A lâmina está prestes a ser içada pelos três cabos mostrados na figura. Substitua o sistema de forças que atua nos cabos por uma força e um momento equivalentes no ponto . A força é vertical.
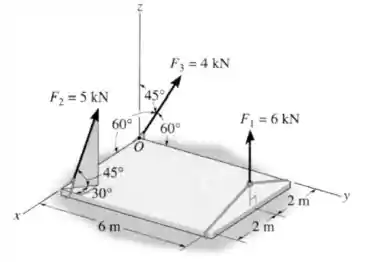
Passo 1
Vamos começar escrevendo cada uma das forças em forma vetorial:
E então a força resultante é:
Passo 2
Agora queremos substituir esse sistema por uma única força (igual à força resultante que acabamos de calcular) aplicada no ponto .
Então precisamos saber qual é o momento total do sistema em relação ao ponto :
Perceba que a força já está sobre o ponto , então o seu momento é nulo em relação a ele.
Agora vamos escrever os dois vetores de posição e :
Na verdade o enunciado não disse qual é a coordenada do ponto de no eixo , mas podemos considerar que é zero, pois não vai fazer diferença no cálculo do momento em relação a !
Passo 3
Agora vamos substituir isso tudo na equação do momento resultante:
Resposta
O sistema pode ser substituído por uma força e por um momento .