Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 180

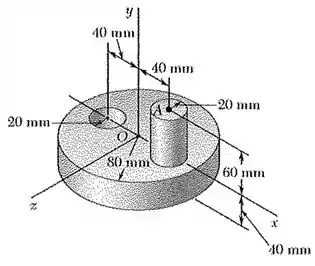
Para o componente descrito no problema 9.165, determine (a) os momentos principais de inércia na origem, (b) os eixos principais de inércia na origem. Esboce o corpo e mostre a orientação dos eixos principais de inércia em relação aos eixos x , y   e   z .

Passo 1

  1. Das soluções do problema 9.165 e 9.141, temos que:

Problema 9.141:

I x = 13.988 × 10 - 3 k g ⋅ m 2

I y = 20.55783 × 10 - 3 k g ⋅ m 2

I z = 13.988 × 10 - 3 k g ⋅ m 2

Problema 9.165:

I y z = I z x = 0

I x y = 0.3946 × - 3 k g ⋅ m 2

Aplicando numa matriz para calcular os momentos principais de inercia:

I x - K - I x y 0 - I x y I y - K 0 0 0 I z - K = 0

Logo,

I x I y - I x + I y K + K 2 - I x y 2 = 0

Substituindo:

K 1 = 14.303 × 10 - 3 k g ⋅ m 2

Logo,

K 2 = 13.96 × 10 - 3 k g ⋅ m 2 e K 3 = 20.6 × 10 - 3 k g ⋅ m 2

Passo 2

Para determinar a direção dos cossenos λ x , λ y , e λ z de cada eixo principal, usaremos as equações abaixo:

I x - K 1 λ x 1 - I x y λ y 1 = 0

- I x y λ x 1 + ( I y - K 1 ) λ y 1 = 0

Substituindo, temos que, para K 1 :

θ x 1 = 90 °

θ y 1 = 90 °

θ z 1 = 0 °

Passo 3

Continuando, vamos determinar para o K 2 :

θ x 2 = 3.4 °

θ y 2 = 86.6 °

θ z 2 = 9 0 °

Continuando, vamos determinar para o K 3 :

θ x 3 = 9 3.4 °

θ y 3 = 3.43 °

θ z 3 = 90 °

Passo 4

Esboçando os eixos:

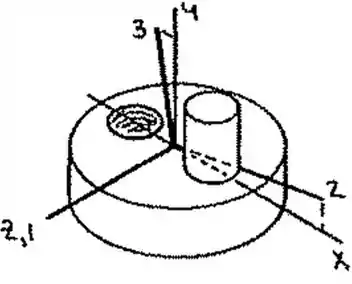
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro