Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 66

Mostre que a resultante das forças hidrostáticas exercidas sobre uma superfície plana submersa de área A é uma força P perpendicular à superfícies cuja intensidade é P = γ A y - sen ⁡ θ = p - A , sendo γ o peso específico do líquido e p - a pressão no centroide C da superfície. Mostre que P é aplicada em um ponto C P , denominado centro de pressões cujas coordenadas são x P = I x y / A y - e y P = I x / A y - , sendo I x y = ∫ x y d A (ver Seção 9.8 ). Mostre também que a diferença de ordenadas y p - y - é igual a k x ' 2 / y - e, portanto, depende da profundidade a que a superfície está submersa.

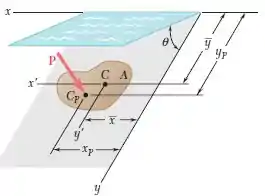
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Consideremos uma profundidade arbitrária:

d = y sen ⁡ θ

A pressão é dada por:

p = γ d

p = γ y sen ⁡ θ

A força hidrostática será:

d P = γ y sen ⁡ θ d A

∑ F = 0

P = ∫ d P

P = ∫ γ y sen ⁡ θ d A

Logo:

P = γ sen ⁡ θ ∫ y d A

P = γ sen ⁡ θ y - A

P = p - A

Passo 2

Temos que:

∑ M x = - y P P = ∫ - y d P

Logo:

- y P P = - γ sen ⁡ θ I x

Ou:

y P = γ sen ⁡ θ I x P

Substituindo, temos que:

y P = γ sen ⁡ θ I x γ sen ⁡ θ y - A

y P = I x y - A

Passo 3

A analise do eixo y nos proporciona:

∑ M y = x P = ∫ x d P

Logo:

x P P = ∫ x γ y sen ⁡ θ d A

x P P = γ sen ⁡ θ ∫ x y d A

Logo:

x P P = γ sen ⁡ θ I x y

Ou:

x P = γ sen ⁡ θ I x y γ sen ⁡ θ y - A

Substituindo, temos que:

x P = I x y y - A

Passo 4

Temos ainda que:

I x = I x ' + A y - 2

I x = A y - y P

I x ' = k - x ' 2 A

Logo:

A y - y P = k - x ' 2 A + A y - 2

Temos que:

y - y P = k - x ' 2 + y - 2

Logo:

k - x ' 2 = y - y P - y - 2

k - x ' 2 = y - y P - y -

Portanto:

k - x ' 2 y - = y P - y -

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro