Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 62
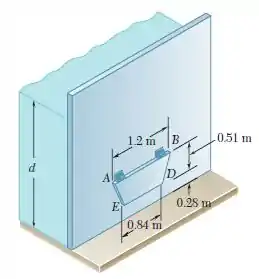
Uma comporta trapezoidal vertical, usda como válvula automática, se mantém fechada por duas molas ligadas a dobradiças localizadas ao longo da aresta . Sabendo que cada mola exerce um binário de intensidade , determine a profundidade da água necessária para que a comporta se abra.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
De acordo com a teoria das resultantes das forças hidrostáticas, temos que:
A distância do centro de pressão em relação à pode ser chamada de . Assim:
Portanto:
E:
Onde é a resultante das forças hidrostáticas agindo na tampa, é a distância até o ponto de aplicação de .
Passo 2
Para a comporta tem-se:
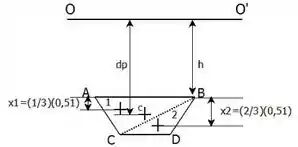
Onde vale a seguinte relação:
Sendo então:
Passo 3
A partir do aspecto construtivo, sabemos que:
Sendo:
E:
Logo:
E:
Passo 4
Para que a comporta abra, temos que:
Resolvendo, temos que:
E: