Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 3.Problemas - Ex. 13
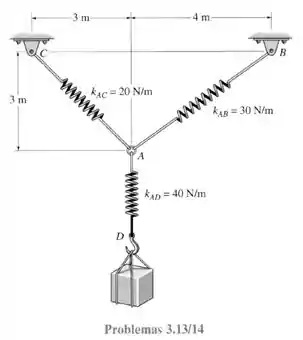
O comprimento sem deformação da mola AB é de 3m. Com o bloco mantido na posição de equilíbrio mostrada, determine a massa dele em D.
Passo 1
Fala aii... beleza??
Nessa questão vamos precisar lembrar da força peso:
A força elástica:
E vamos mandar um diagrama de corpo livre maroto:
E pra matar a questão, como está em equilíbrio, então o somatório das forças é igual a zero:
Passo 2
Vamos achar primeiro o seno e o cosseno desses ângulos porque vamos precisar.
No triângulo da esquerda podemos usar Pitágoras para achar :
Daí temos:
E no triângulo da direita pra achar :
Daí:
Passo 3
Agora é só ser feliz decompondo as forças e jogando no somatório.
- Em :
Como sabemos que o comprimento da mola sem deformação é igual a e o comprimento de AB na figura é , então:
Então conseguimos achar :
- Em :
Substituindo os valores:
E acabamos mais uma questãozinha...
Mas bora pra próxima treinar mais?