Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 164

O cone circular homogêneo mostrado na figura tem massa m . Determine o produto de inércia do cone em relação à linha que liga a origem O e o ponto A .

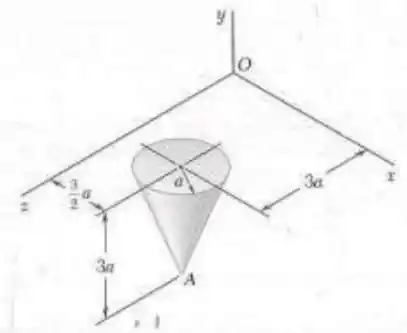
Passo 1

Primeiramente vamos calcular o valor da distância entre O a A e encontraremos

d O A = 3 a 2 2 + - 3 a 2 + 3 a 2 = 9 a 2

Então

λ O A = 1 9 a 2 ⋅ 3 2 a i - 3 a j + 3 a k = 1 3 ⋅ i - 2 j + 2 k

Passo 2

No sistema de coordenadas retangular com a origem no ponto A e alinhado com os eixos x , y   e   z nós temos

I x = I z = 3 5 ⋅ m ⋅ a 2 4 + 3 a 2 = 111 20 ⋅ m a 2   e   I y = 3 10 ⋅ m a 2

Pela simetria do problema podemos inferir que

I x y = I y z = I z x = 0

Como os produtos de inércia são iguais a 0 , nossa equação se reduz a

I O A = I x ⋅ λ x 2 + I y ⋅ λ y 2 + + I z ⋅ λ z 2

I O A = 111 20 ⋅ m a 2 ⋅ 1 3 2 + 3 10 ⋅ m a 2 ⋅ - 2 3 2 + 111 20 ⋅ m a 2 ⋅ 2 3 2

I O A = 193 60 ⋅ m a 2

Resposta

I O A = 193 60 ⋅ m a 2

Ver Outros Exercícios desse livro