Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 165

A figura mostra o elemento de máquina do problema 9.141 . Determine seus momentos de inércia em relação à linha que liga a origem O e o ponto A .

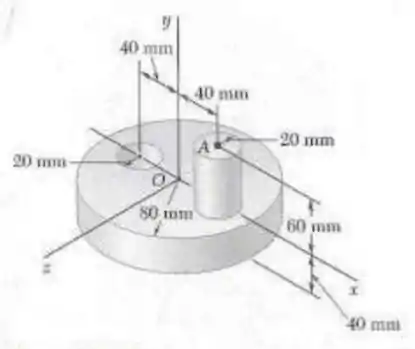
Passo 1

Vamos, antes de tudo, dividir o nosso corpo em 3 partes dadas por

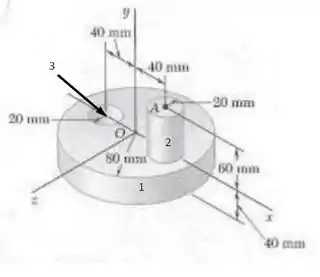
Calculando a massa de cada uma das partes vamos obter

m 1 = 7850 ⋅ π ⋅ 0.08 2 ⋅ 0.04 ≈ 6.31334   k g

m 2 = 7850 ⋅ π ⋅ 0.02 2 ⋅ 0.06 ≈ 0.59188   k g

m 3 = 7850 ⋅ π ⋅ 0.02 2 ⋅ 0.0 4 ≈ 0.39458   k g

Pela simetria do nosso corpo vamos ter

I y z = I z x = 0 ,     I x ' y ' - 2 = I x ' y ' - 3 = 0 ,   I x y 1 = 0

Além disso, da solução do problema 9.141 temos

I x = 13.988 ⋅ 10 - 3 k g ⋅ m 2

I y = 20.55783 ⋅ 10 - 3 k g ⋅ m 2

I z = 14.30368 ⋅ 10 - 3 k g ⋅ m 2

E por inspeção/observação notamos que

λ O A = 1 13 ⋅ 2 i + 3 j

Passo 2

Assim, conseguimos calcular

I x y = ∑ I x ' y ' - + m x - y - = m 2 ⋅ x 2 - ⋅ y 2 - - m 3 ⋅ x 3 - ⋅ y 3 -

I x y = 0.59188 ⋅ 0.04 ⋅ 0.03 - 0.39458 ⋅ - 0.04 ⋅ - 0.02 ≈ 0.3946 ⋅ 10 - 3   k g ⋅ m 2

Assim a equação que vai nos fornecer o momento de inércia desejado é dada por

I o a = I x ⋅ λ x 2 + I y ⋅ λ y 2 + I z ⋅ λ z 2 - 2 I x y ⋅ λ x ⋅ λ y - 2 I y z ⋅ λ y ⋅ λ z - 2 I z x ⋅ λ z ⋅ λ x

= 13.988 ⋅ 2 13 2 + 20.55783 ⋅ 3 13 2 - 2 ⋅ 0.3946 ⋅ 2 13 ⋅ 2 13 ⋅ 10 - 3 k g ⋅ m 2

I o a ≈ 18.17 ⋅ 10 - 3 k g ⋅ m 2

Resposta

I O A = 18.17 ⋅ 10 - 3   k g ⋅ m 2

Ver Outros Exercícios desse livro