Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 151

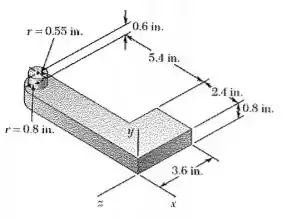
Determine os produtos e inércia I x y ,   I y z   e   I z x da peça de máquina de alumínio fundido mostrado na figura. (A massa específica do aço é 0.1 l b / i n 3 ).

Passo 1

Primeiramente, vamos dividir nossa peça em 4 partes dadas por

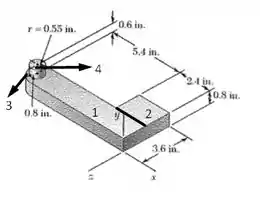
Agora, vamos calcular a massa de cada componente que é dada por

m = ρ A l ⋅ V = γ A l g ⋅ V

Então

M 1 = 0.1 32.2 ⋅   7.8 ⋅ 0.8 ⋅ 1.6 ≈ 31 ⋅ 10 - 3 l b ⋅ s 2 / f t

M 2 = 0.1 32.2 ⋅ 2.4 ⋅ 0.8 ⋅ 2 = 11.9255 ⋅ 10 - 3 l b ⋅ s 2 / f t

M 3 = 0.1 32.2 ⋅ π 2 ⋅ 0.8 2 ⋅ 0.8 = 2.4977   l b ⋅ s 2 / f t

M 4 = 0.1 32.2 ⋅ π ⋅ 0.55 2 ⋅ 0.6 = 1.77   l b ⋅ s 2 / f t

Além disso, por conta da simetria presente na figura temos que os produtos de inércia I x ' y ' - = I y ' z ' - = I z ' x ' - serão iguais a zero. Temos ainda

x 3 - = - 7.8 + 4 ⋅ 0.8 3 π = - 8.13953   i n

Passo 2

Com as informações adquiridas até agora podemos construir a seguinte tabela

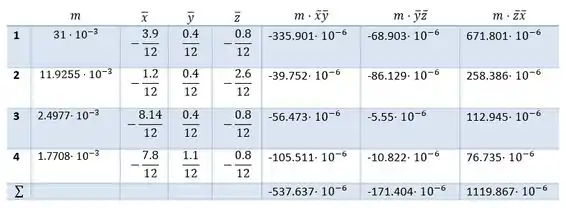
Então com a tabela acima em mãos podemos determinar os produtos de inércia de uma forma mais simples fazendo

I x y = ∑ I x ' y ' - + m x y - → I x y = - 538 ⋅ 10 - 6 l b ⋅ f t ⋅ s 2

I y z = ∑ I y ' z ' - + m y z - → I y z = - 171.4 ⋅ 10 - 6 l b ⋅ f t ⋅ s 2

I z x = ∑ I z ' x ' - + m z x - → I z x = 1120 ⋅ 10 - 6 l b ⋅ f t ⋅ s 2

Resposta

I x y = - 538 ⋅ 10 - 6 l b ⋅ f t ⋅ s 2

I y z = - 171.4 ⋅ 10 - 6 l b ⋅ f t ⋅ s 2

I z x = 1120 ⋅ 10 - 6 l b ⋅ f t ⋅ s 2

Ver Outros Exercícios desse livro