Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 174

Para o cone circular do problema resolvido 9.11 , determine o valor da razão a h para que o elipsoide de inércia do cone seja uma esfera quando calculado a no vértice do cone, b no centro da base do cone.

Passo 1

A figura da qual estamos falando é a seguinte

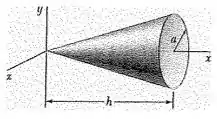
Do problema citado no enunciado temos que na extremidade do cone teremos

I x = 3 10 ⋅ m a 2

I y = I z = 3 5 ⋅ m ⋅ a 2 4 + h 2

E pela simetria do problema I x y = I y z = I z x = 0 . Utilizando a equação do elipsoide de inércia vamos ter

I x ' ⋅ x 2 + I y ' ⋅ y 2 + I z ' ⋅ z 2 = 1

→   3 10 ⋅ m a 2 ⋅ x 2 + 3 5 ⋅ m ⋅ a 2 4 + h 2 ⋅ y 2 + 3 5 ⋅ m ⋅ a 2 4 + h 2 ⋅ z 2 = 1

Para que o elipsoide de inércia seja uma esfera devemos ter que os coeficientes sejam iguais. Assim,

3 10 ⋅ m a 2 = 3 5 ⋅ m ⋅ a 2 4 + h 2 → a h = 2  

Passo 2

De forma análoga ao que foi feito acima vamos calcular para o centro da base do nosso cone. Então, teremos

I x ' = 3 10 ⋅ m a 2

E no centroide do nosso cone temos

I y ' = 3 20 m ⋅ a 2 + h 2 4

Dessa forma, aplicando o teorema dos eixos paralelos para o ponto que nos interessa teremos

I y ' = I z ' = 3 20 m ⋅ a 2 + h 2 4 + m ⋅ h 4 2 = 1 20 ⋅ m ⋅ 3 a 2 + 2 h 2

Novamente pela simetria vamos ter I x y = I y z = I z x = 0 . Por fim, igualando os coeficientes vamos obter

3 10 ⋅ m a 2 = 1 20 ⋅ m ⋅ 3 a 2 + 2 h 2 → a h = 2 3

E finalmente, resolvemos nosso problema.

Resposta

a   a h = 2  

b a h = 2 3

Ver Outros Exercícios desse livro