Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 171
Para a estrutura e o carregamento mostrador na figura, determine as reações em , considere que na superfície de cada apoio não há atrito.
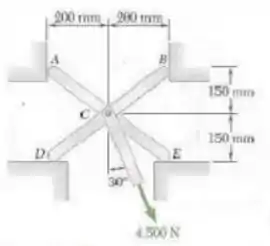
Passo 1
Para conseguirmos determinar as reações nos pontos indicados e desejados pelo enunciado vamos nos valer das condições de equilíbrio primeiramente para a estrutura inteira de tal forma que teremos
Passo 2
Analisando, agora, o membro vamos ter
Fazendo o mesmo para o membro teremos
Substituindo em vamos obter
Por fim, conseguimos encontrar o valor de somando as equações
Resposta
Exercícios de Livros Relacionados
Três livros uniformes, cada um com peso W e comprimento a , são empilhados como na figura. Determine a distância máxima d que o livro do topo pode estender-se em relação ao da base, de modo que a pilh
O atuador pneumático em D é usado para aplicar uma força de F sobre o membro em B . A reação normal do eixo liso em C sobre o membro é de 300 N. Determine a intensidade de F e as componentes horizonta
Determine as reações no pino A e a tração no cabo B C . Considere F = 40k N . Desconsidere a espessura da viga.
Uma tira de metal rígida, com peso desprezível, é usada como parte da chave eletromagnética. Se a rigidez das molas em A e B for k = 5N / m e a tira estiver originalmente horizontal quando as molas es
Determine a distância d para a posição da carga P para que haja equilíbrio da haste lisa na posição θ , como mostra a figura. Desconsidere o peso da haste.