Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 169

Determine o momento de inércia de massa do componente da máquina dos problemas 9.136 e 9.155 em relação ao eixo que passa pela origem caracterizado pelo vetor unitário λ = - 4 i + 8 j + k 9 .

Passo 1

O componente de máquina que é descrito nas questões 9.136 e 9.155 é o seguinte

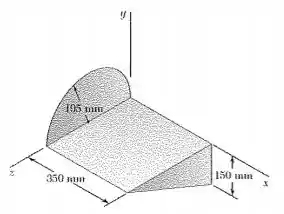
Além disso, dessas questões temos que

I x = 175.503 ⋅ 10 - 3   k g ⋅ m 2

I y = 308 ⋅ 629 ⋅ 10 - 3   k g ⋅ m 2

I z = 154.4 ⋅ 10 - 3   k g ⋅ m 2

I x y = - 8.0365 ⋅ 10 - 3   k g ⋅ m 2

I y z = 12.895 ⋅ 10 - 3   k g ⋅ m 2

I z x = 94.0266 ⋅ 10 - 3     k g ⋅ m 2

Passo 2

Assim a equação que vai nos fornecer o momento de inércia desejado é dada por

I o l = I x ⋅ λ x 2 + I y ⋅ λ y 2 + I z ⋅ λ z 2 - 2 I x y ⋅ λ x ⋅ λ y - 2 I y z ⋅ λ y ⋅ λ z - 2 I z x ⋅ λ z ⋅ λ x

I O L = 175.503 ⋅ - 4 9 2 + 308.629 ⋅ 8 9 2 + 154.4 ⋅ 1 9 2 - 2 ⋅ - 8.0365 ⋅ - 4 9 ⋅ 8 9 - 2 ⋅ 12.895 ⋅ 8 9 ⋅ 1 9 - 2 ⋅ 94.0266 ⋅ 1 9 ⋅ - 4 9 ⋅ 10 - 3   k g ⋅ m 2

I o L ≈ 281 × 10 - 3   k g ⋅ m 2

Resposta

I o l = 281 ⋅ 10 - 3   k g ⋅ m 2

Ver Outros Exercícios desse livro