Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 71

O cone está rotacionando a uma taxa constante ω s = 150   r a d / s . Determine a taxa constante ω p na qual ele realiza uma precessão se ϕ = 30 °

Passo 1

Nesse exercício, iremos primeiramente analisar o esquema a seguir:

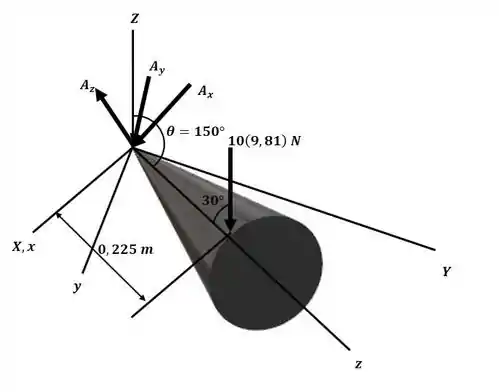
Com base nele e nas informações fornecidas no enunciado, temos:

θ = 180 - 30 = 150 °

ψ ˙ = ω s = - 150   r a d / s

E sabemos também que ϕ ˙ = ω p são constantes.

Passo 2

Sendo assim, podemos agora calcular o momento de inércia do sistema em relação aos eixos principais:

I z = 3 10 10 0,1 2 → I z = 0,03   k g . m 2

I = I x = I y = 3 80 10 4 0,1 2 + 0,3 2 + 10 0,225 2

I = I x = I y = 0,555   k g . m 2

Passo 3

Sendo assim, podemos aplicar a equação de momento com relação ao eixo x:

∑ M x = - I ϕ ˙ 2 s e n θ c o s θ + I z ϕ ˙ s e n θ ( ϕ ˙ c o s θ + ψ ˙ )

- 10 9,81 s e n 30 ° 0,225 = - 0,555 ω p 2 s e n 150 ° c o s 150 ° + 0,03 ω p s e n 150 ° [ ω p c o s 150 ° + ( - 150 ) ]

0,02273 ω p 2 - 2,25 ω p + 11,036 = 0

Resolvendo essa equação do 2° grau, obtemos duas velocidades possíveis:

ω p = 13,5   r a d / s

ω p = 3,6   r a d / s

Resposta

ω p = 13,5   r a d / s

ω p = 3,6   r a d / s

Ver Outros Exercícios desse livro