Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 73
No momento da decolagem, o trem de pouso de um avião é recolhido com uma velocidade angular constante , enquanto a roda continua a girar. Se o avião decola com uma velocidade , determine o torque em A em decorrência do efeito giroscópico. A roda tem uma massa de 50 kg e o raio de giração em relação a seu eixo de rotação é k = 300 mm.
Passo 1
Começaremos o exercício convertendo a velocidade do avião para m/s:
Sendo assim, podemos escrever a velocidade angular com que a roda gira da seguinte forma:
Passo 2
Agora, com o auxílio do diagrama representativo da roda a seguir podemos encontrar os valores de interesse para aplicar as equações de momento:
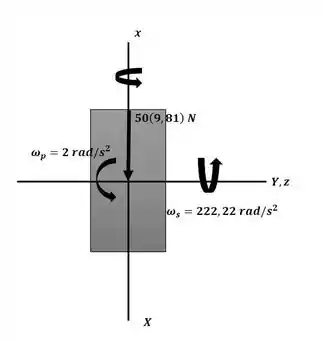
Com base no diagrama:
Agora iremos calcular o momento de inércia do sistema com relação ao eixo z:
Passo 3
Sendo assim, podemos aplicar a equação de momento com relação ao eixo x: