Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 2.Problemas - Ex. 21

Um conjunto de quatro hastes rígidas sem peso e uma mola é organizado de dois modos diferentes para suportar um peso W , como mostrado na Figura 2.51. Determine as frequências naturais de vibração dos dois esquemas.

Passo 1

Fala, galera!

Então, pra resolver essa questão vamos ser dividi-la em 2 etapas, uma pra cada um dos esquemas!

Sendo b a distância da diagonal maior do losango das figuras, temos que b   =   2 l   s e n θ .

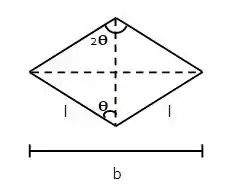
1ª Etapa

Nesse caso, primeiro precisamos encontrar a constante elástica pela equivalência da energia potencial:

1 / 2   k e q ⋅ x 2   =   1 / 2   k ⋅ x b 2

k e q =   k ⋅ ( x b / x ) 2

Onde,

x = deslocamento da massa

x b = deslocamento da mola

Passo 2

Sabendo que a distância da diagonal menor, sem nenhum deslocamento em x, é   l 2 - b 2 2 , temos que:

x   = 2     l 2 - b - x b 2 2 -   l 2 - b 2 2

e resolvendo essa conta enorme ai e partindo pro que realmente importa, encontramos:

x   =   b ⋅ x b 2   ( l 2 - b 2 4 ) 1 2  

Assim,

k e q   =   k ⋅ 2 x b ( l 2 - b 2 4 ) 1 2 b ⋅ x b   2 =   k ⋅ 4 l 2 - b 2 b 2

k e q =   k ⋅ 4 l 2 - 2 l   s e n θ 2 2 l   s e n θ 2   =     k ⋅ 4 l 2 - 4 l 2   s e n 2 θ 4 l 2   s e n 2 θ

k e q   =   k   c o s 2 θ s e n 2 θ   =   k ⋅ c o t g 2 θ

Então sua frequência natural

w n = k e q m   =     k ⋅ g ⋅ c o t g 2 θ W

Passo 3

2ª Etapa

Já nesse caso, como a o deslocamento de W ( x ) é igual a deformação da mola ( x b ), temos que k e q   =   k , então

w n   =     k ⋅ g W

Bem mais rapidinha essa, né!?

Resposta

Frequência natural do esquema (a)

w n =     k ⋅ g ⋅ c o t g 2 θ W

Frequência natural do esquema (b)

w n   =     k ⋅ g W  

Ver Outros Exercícios desse livro