Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 2.Problemas - Ex. 12

Determine a frequência natural do sistema mostrado na Figura 2.44 com e sem as molas k 1 e k 2 no ponto médio da viga elástica.

Passo 1

Vamos lá!

Primeiramente, vamos calcular qual seria a frequência natural com as molas k 1 e k 2 .

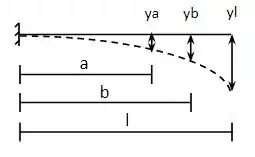
Sendo y a , y b , y l as deflexões da viga nas distâncias a , b e l , a partir da ponta engastada, temos que

Para encontrarmos a constante elástica equivalente das molas k 1 e k 2 utilizamos a fórmula de energia potencial elástica

1 2 ⋅ k e q 12 ⋅ y l 2   = 1 2 ⋅ k 1 ⋅ y a 2 + 1 2 ⋅ k 2 ⋅ y b 2

k e q 12 =   k 1 ⋅ y a y l ²   +   k 2 ⋅ y b y l   ²

Nesta questão, além da constante elástica das molas, também temos que trabalhar com a constante elástica da viga, que por estar em balanço é

k v i g a = 3 E I l 3

(lembrando que esta é uma fórmula tabelada)

Passo 2

Já a deflexão de uma viga com engaste em balanço pode ser calculada por

y   = F x 2 6 E I   ⋅ ( 3 l - x )

Ou seja,

x   =   a     →     y a   = F a 2 6 E I   ⋅ ( 3 l - a )

x   =   b     →     y b   = F b 2 6 E I   ⋅ ( 3 l - b )

x   =   l     →     y l   = F l 3 3 E I

Agora vamos juntar todas essas informações para encontrar a constante elástica equivalente

k e q   =   k e q 12 ⋅ k v i g a k e q 12 +   k v i g a

k e q =     k 1 ⋅ y a y l 2 +   k 2 ⋅ y b y l 2 k v i g a   k 1 ⋅ y a y l 2 +   k 2 ⋅ y b y l 2 + k v i g a

E a sua frequência natural

w n   =   k 1 ⋅ y a y l 2 +   k 2 ⋅ y b y l ⋅ 3 E I l 3 m   k 1 ⋅ y a y l 2 +   k 2 ⋅ y b y l 2 + 3 E I l 3 1 2  

w n   =     k 1 ⋅ a 4   ( 3 l - a ) 2 ⋅ 3 E I + k 2 ⋅ b 4 ( 3 l - b ) 2 ⋅ 2 E I k 1 ⋅ a 4   3 l - a ) 2 + k 2 ⋅ b 4 3 l - b 2 + 12 E I ⋅ l 3 1 2

UFA!!! Muita letra e confusão, mas é só substituir direitinho e fazer com atenção que vai dar tudo certo no final!

Passo 3

KKKKK pensou que acabou?

Pera que tá quase!

A questão também pede para encontrar w n sem nenhuma das molas k 1 e k 2 , mas agora é rapidinho. Se ele quer o valor sem as molas, apenas utilizaremos a constante elástica da viga, ou seja

w n   =   k v i g a m   =   3 E I m l 3

Agora sim, fim!

Bora pra próxima!!

Resposta

Frequência natural

Com as molas k 1 e k 2 :

w n   =     k 1 ⋅ a 4   ( 3 l - a ) 2 ⋅ 3 E I + k 2 ⋅ b 4 ( 3 l - b ) 2 ⋅ 2 E I k 1 ⋅ a 4   3 l - a ) 2 + k 2 ⋅ b 4 3 l - b 2 + 12 E I ⋅ l 3 1 2

Sem as molas k 1 e k 2 :

w n   =   3 E I m l 3

Ver Outros Exercícios desse livro