Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 9.Problemas - Ex. 64

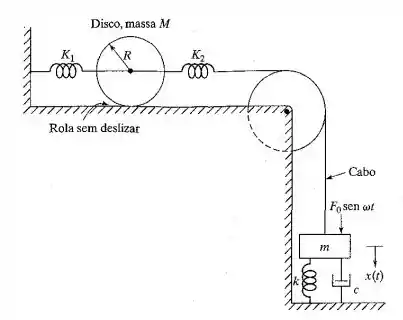
Considere o sistema mostrado na Figura 9.46 no qual uma força harmônica age sobre a massa m. Deduza a condição sob a qual o deslocamento da massa m em regime permanenteserá zero.

Passo 1

Alô Alô tranquilooo??

Só vamooo!!!

Arrasta pra cimaaaa

O sistema de vibração possui configuração conforma mostrado :

Passo 2

As equações do movimento das massas m e M são:

m x ¨ + c x ˙ + K 1 + K 2 x - K 2 x 2 = F 0 s e n ( ω t )

M x ¨ 2 + K 1 + K 2 x 2 - K 2 x = 0             ( 1 )

Ao assumir uma solução harmônica da forma

x j = X j cos ⁡ ( ω t )

Com j = 1,2

A equação (1) pode dar a equação da amplitude como:

K 1 + K 2 - m ω 2 - c ω X - K 2 X 2 = F 0

K 1 + K 2 - M ω 2 X 2 - K 2 C = 0

Passo 3

Ou pode ser expresso na equação da matriz como

K 1 + K 2 - m ω 2 - c ω - K 2 - K 2 K 1 + K 2 - M ω 2 X X 2 = F 0 0

A solução de amplitude X   e   X 2 são

X = K 1 + K 2 - m ω 2 - c ω F 0 K 1 + K 2 - m ω 2 - c ω K 1 + K 2 - M ω 2 - K 2 2

X 2 = K 2 F 0 K 1 + K 2 - m ω 2 - c ω K 1 + K 2 - M ω 2 - K 2 2

A transmissibilidade da amplitude é expressa como

T d = X X 2 = K 1 + K 2 - m ω 2 - c ω K 2

A condição X será zero, se essa condição for satisfeita

K 1 + K 2 - m ω 2 - c ω = 0

Resposta

Vide o passo a passo.

Ver Outros Exercícios desse livro