Construa os gráficos de em relação a e de em relação a quando varia de 0 a 1,0 e .
Passo 1
Alô Alô tranquilooo??
Só vamooo!!!
Arrasta pra cimaaaa
Então, nesse caso, as equações de frequência natural do nosso sistema assumem as forma abaixo, onde é a massa do absorvedor para a relação da massa do sistema inicial enquanto são frequências naturais do sistema combinado.
A primeira frequência natural pode ser calculada usando a equação abaixo, onde é a razão da massa do absorvedor para a massa inicial do sistema e é a frequência natural do absorvedor
Como exemplo, calcularemos o valor de para , usando a seguinte expressão:
O valor de para , é de 0.85.
Passo 2
A tabela a seguir mostra o resultado do cálculo usando a expressão (1), para um determinado intervalo de
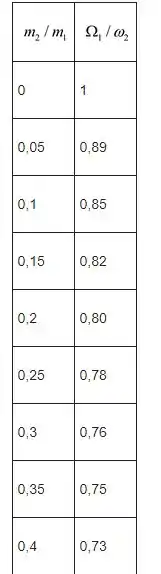
A relação gráfica entre é mostrada na figura a seguir:
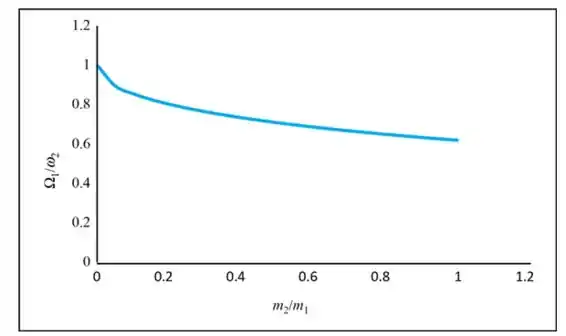
Passo 3
A segunda frequência natural pode ser calculada usando a equação abaixo, onde é a razão da massa do absorvedor para a massa inicial do sistema e é a frequência natural do absorvedor
Como exemplo, calcularemos o valor de para , usando a seguinte expressão:
O valor de para , é de 1.17
Passo 4
A tabela a seguir mostra o resultado do cálculo usando a expressão (2), para um determinado intervalo de
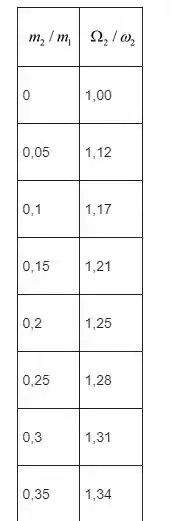
A relação gráfica entre é mostrada na figura a seguir:
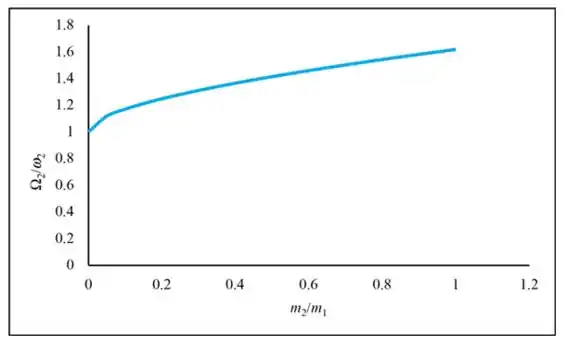
Resposta
Vide o passo a passo.