Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 8.Problemas - Ex. 11

Se uma corda de comprimento l , fixa em ambas as extremidades, sofrer um deslocamento transversal inicial de h em x   =   l / 3 e entao for solta, determine seu movimento subseqliente. Compare as formas de deflexao da corda nos tempos t   =   0 , l 4 c , l 3 c , l 2 c   e considerando os quatro primeiros termos da solução da série.

Passo 1

E aí, galerinha!

Bom! Bora lá! Vamos começar fazendo um esboço do nosso problema...

Pela equação 8.30 , temos que...

W x , t = ∑ n = 1 ∞ τ n sen ⁡ n π x l cos ⁡ n c π t l   ( i )

Onde...

τ n = 2 l ∫ 0 l W 0 x sen ⁡ n π x l d x   ( i i )

A deflexão inicial da barra sabemos que é dada por...

W 0 x = 3 h x l   p a r a   0 ≤ x ≤ l 3 3 h ( l - x ) 2 l   p a r a l 3 ≤ x ≤ l     ( i i i )

Passo 2

Subsituindo a equação ( i i i ) em ( i i ) , a integral então passa a ser dada por...

τ n = 2 l ∫ 0 l W 0 x sen ⁡ n π x l d x

τ n = 2 l ∫ 0 l 3 3 h x l   sen ⁡ n π x l d x + ∫ l 3 l 3 h ( l - x ) 2 l   sen ⁡ n π x l d x

Resolvendo essa integral...

τ n = 2 l ∫ 0 l 3 3 h x l   sen ⁡ n π x l d x + ∫ l 3 l 3 h ( l - x ) 2 l   sen ⁡ n π x l d x

τ n = 6 h l 2 l 2 n 2 π 2 sen ⁡ n π x l - x l n π cos ⁡ n π x l 0 l 3 - 3 h l ⋅ l n π cos ⁡ n π x l l 3 l - 3 h l 2 l 2 n 2 π 2 sen ⁡ n π x l - x l n π cos ⁡ n π x l l 3 l

τ n = 9 h n 2 π 2 sen ⁡ n π 3

Passo 3

Bom! Agora vamos testar valores...

  • Para n = 1 :

    • τ n = 9 h 1 2 π 2 sen ⁡ π 3 = 9 h 3 2 π 2

  • Para n = 2 :

    • τ n = 9 h 2 2 π 2 sen ⁡ 2 π 3 = 9 h 3 8 π 2

  • Para n = 3 :

    • τ n = 9 h 3 2 π 2 sen ⁡ 3 π 3 = 0

  • Para n = 4 :

    • τ n = 9 h 4 2 π 2 sen ⁡ 4 π 3 = 9 h 3 32 π 2

  • Para n = 5 :

    • τ n = 9 h 5 2 π 2 sen ⁡ 5 π 3 = 9 h 3 50 π 2

  • Para n = 6 :

    • τ n = 9 h 6 2 π 2 sen ⁡ 6 π 3 = 0

    ⋮

    ⋮

    Dessa forma, podemos escrever W ( x , t ) como...

    W x , t = 9 3 2 π 2 h sen ⁡ π x l cos ⁡ c π t l + 9 3 8 π 2 h sen ⁡ 2 π x l cos ⁡ 2 c π t l - 9 h 3 32 π 2 sen ⁡ 4 π x l cos ⁡ 4 c π t l - ⋯

    Passo 4

    Aí sim, rapaziada!

    Vamos então, achar as condições de contorno!

    Para t = 0 , temos que W ( x , 0 ) vai valer...

    W x , 0 = 9 3 2 π 2 h sen ⁡ π x l cos ⁡ c π 0 l + 9 3 8 π 2 h sen ⁡ 2 π x l cos ⁡ 2 c π 0 l - 9 h 3 32 π 2 sen ⁡ 4 π x l cos ⁡ 4 c π 0 l - ⋯

    W x , 0 = 9 3 2 π 2 h sen ⁡ π x l + 9 3 8 π 2 h sen ⁡ 2 π x l - 9 3 32 π 2 h sen ⁡ 4 π x l - 9 3 50 π 2 h sen ⁡ 5 π x l ⋯

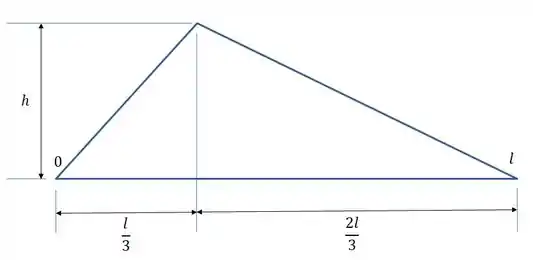
    Dessa forma, a nossa curva fica assim...

  • P a r a   t = l 4 c :

    • W x , l 4 c = 9 3 2 π 2 h sen ⁡ π x l cos ⁡ c π l 4 c l + 9 3 8 π 2 h sen ⁡ 2 π x l cos ⁡ 2 c π l 4 c l - 9 3 32 π 2 h sen ⁡ 4 π x l cos ⁡ 4 c π l 4 c l ⋯

    W x , l 4 c = 9 3 2 π 2 h 2   sen ⁡ π x l - 9 3 32 π 2 h sen ⁡ 4 π x l + 9 3 50 π 2 h 2   sen ⁡ 5 π x l

  • P a r a   t = l 3 c :

    • W x , l 3 c = 9 3 2 π 2 h sen ⁡ π x l cos ⁡ c π l 3 c l + 9 3 8 π 2 h sen ⁡ 2 π x l cos ⁡ 2 c π l 3 c l - 9 3 32 π 2 h sen ⁡ 4 π x l cos ⁡ 4 c π l 3 c l ⋯

    W x , l 3 c = 9 3 h 4 π 2   sen ⁡ π x l - 1 4 sen ⁡ 2 π x l + 1 16   sen ⁡ 4 π x l - 1 25 sen ⁡ 5 π x l

  • P a r a   t = l 2 c :

    • W x , l 3 c = 9 3 2 π 2 h sen ⁡ π x l cos ⁡ c π l 2 c l + 9 3 8 π 2 h sen ⁡ 2 π x l cos ⁡ 2 c π l 2 c l - 9 3 32 π 2 h sen ⁡ 4 π x l cos ⁡ 4 c π l 2 c l ⋯

    W x , l 3 c = - 9 3 h 8 π 2   sen ⁡ 2 π x l + 1 4 sen ⁡ 4 π x l

  • P a r a   t = l c :

    • W x , l 3 c = 9 3 2 π 2 h sen ⁡ π x l cos ⁡ c π l c l + 9 3 8 π 2 h sen ⁡ 2 π x l cos ⁡ 2 c π l c l - 9 3 32 π 2 h sen ⁡ 4 π x l cos ⁡ 4 c π l c l ⋯

    W x , l 3 c = 9 3 h 2 π 2 -   sen ⁡ π x l + 1 4 sen ⁡ 2 π x l - 1 16   sen ⁡ 4 π x l + 1 25 sen ⁡ 5 π x l

    Resposta

  • P a r a   t = l 4 c

    • W x , l 4 c = 9 3 2 π 2 h 2   sen ⁡ π x l - 9 3 32 π 2 h sen ⁡ 4 π x l + 9 3 50 π 2 h 2   sen ⁡ 5 π x l

  • P a r a   t = l 3 c

    • W x , l 3 c = 9 3 h 4 π 2   sen ⁡ π x l - 1 4 sen ⁡ 2 π x l + 1 16   sen ⁡ 4 π x l - 1 25 sen ⁡ 5 π x l

  • P a r a   t = l 2 c

    • W x , l 3 c = - 9 3 h 8 π 2   sen ⁡ 2 π x l + 1 4 sen ⁡ 4 π x l

  • P a r a   t = l c

W x , l 3 c = 9 3 h 2 π 2 -   sen ⁡ π x l + 1 4 sen ⁡ 2 π x l - 1 16   sen ⁡ 4 π x l + 1 25 sen ⁡ 5 π x l

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro