Determine a solução de vibração livre de uma corda fixa em ambas as extremidades sob as condições iniciais e .
Passo 1
E aí, galerinha!
Bom! Bora lá pro que interessa!
Antes de mais nada, vamo pra uma introduçãozinha!
Pra corda fixa em ambas as extremidades, temos a seguinte situação mostrada na figura abaixo...
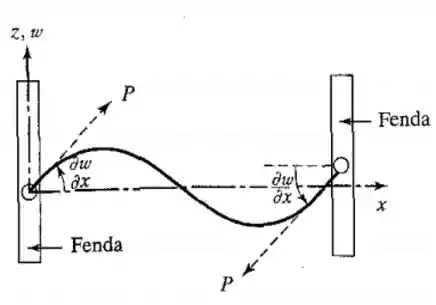
E outra coisa que a gente sabe da nossa bibliografia, é que a solução geral nas condições de contorno dadas por...
É igual à...
Onde...
Passo 2
Pois muito bem! Já sabemos que uma das condições de contorno é...
Logo, substituindo na fórmula, obtemos que... A maior possibilidade disso aí dar zero é quando...
Ficamos então, com...
Passo 3
Pois muito bem! Sabemos que a outra condição dada é...
Subsituindo isso na fórmula do :
Obtemos a seguinte fórmula acima!
Passo 4
Agora se liga nessa fórmula abaixo pra calcular a integral do produto de dois senos...

Por essa fórmula, para temos que...
E para
- Para :
- Para :
Dessa forma, obtemos que...
E então, a nossa fórmula final vai ficar assim...