Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.10 - Ex. 119
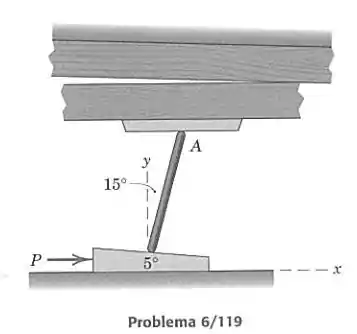
A cunha com cavilha é um dispositivo eficiente para fechar o vão entre duas pranchas, durante a construção de um barco de madeira. Para a combinação mostrada, se uma força é requerida para mover a cunha, determine a força de atrito que atua na extremidade superior da cavilha. O coeficiente de atrito estático e dinâmico para todos os pares de superfície em contato vale 0,40.
Passo 1
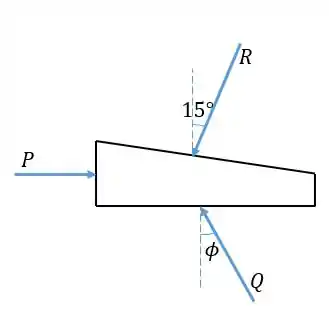
Vamos isolar a cunha em um diagrama de corpo livre. Atuam nela três forças: a força horizontal, a força feita pelo contato com o solo e a força causada pela barra. A força , que é composta por normal e atrito, deve possuir um ângulo em relação à horizontal igual ao ângulo de atrito , que satisfaz a seguinte relação:
A força causada pela barra tem angulação de 15° com a vertical, e o que queremos é determinar a componente horizontal dessa força, pois como a barra é um elemento de duas forças, a mesma força horizontal na parte de baixo deve ser sofrida na parte de cima em .
Passo 2
Primeiro vamos determinar o ângulo de atrito . A tangente desse ângulo deve ser igual ao coeficiente de atrito:
Então colocamos as três forças num triângulo de forças:
Passo 3
Queremos o valor da força . Podemos obtê-lo usando a Lei dos Senos, que diz que num triângulo a razão entre o seno de um ângulo e o tamanho lado oposto é a mesma para os três ângulos. Vamos usar a lei para e :
Mas queremos a componente horizontal dessa força, que é a força de atrito entre a caavilha em e a placa acima dela. Como a inclinação da barra é de 15°: