Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 169
169- O cabo móvel para o teleférico de uma rampa de esqui tem uma massa de e suporta cadeiras e passageiros igualmente espaçados, cuja massa extra é de quando se faz uma média sobre todo o comprimento do cabo. O cabo puxa horizontalmente a partir da roda-guia de sustentação em . Calcule as forças trativas no cabo em e e o comprimento do cabo entre e .
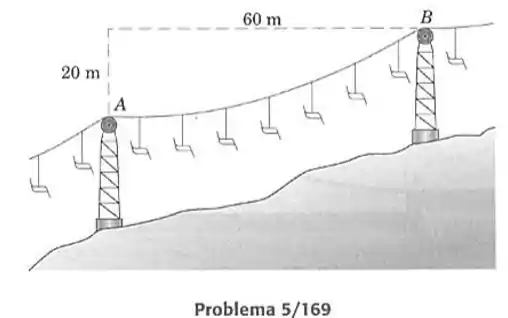
Passo 1
O peso específico da corda do cabo pode ser aproximado para o peso do específico do cabo somada com a das cadeiras, o que nos dará um cabo equivalente com densidade igual a:
Passo 2
Como o cabo encontra-se na horizontal na posição podemos dizer que temos uma catenária na posição de em , o que nos diz que em estamos na posição além de que a tração na origem do sistema é a tração em igual a , logo em temos a seguinte equação de catenária:
Numericamente encontramos um valor igual a:
Passo 3
Em então vamos ter uma força de tração igual a:
Passo 4
O comprimento da catenária indo da origem até o ponto nos dá o tamanho . Onde tem a seguinte equação:
Logo ela valerá: