Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 59
Uma cunha cônica é colocada entre duas placas horizontais que, em seguida, são movidas vagarosamente uma em direção à outra. Indique o que acontecerá com a cunha se se .
Passo 1
Vamos começar esse excercício desenhando o diagrama de corpo livre para a cunha:
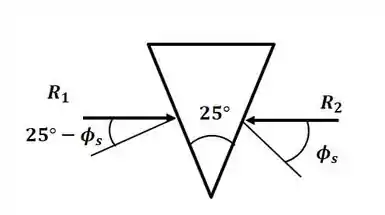
Conforme vimos na seção anterior do livro, o coeficiente de atrito pode ser encontrado através de:
Substituindo o valor dado de :
Passo 2
Vamos analisar primeiro o caso da letra em que . Conforme vimos na seção anterior do livro, o coeficiente de atrito pode ser encontrado através de:
Substituindo o valor dado de :
Então, voltando para o DCL do passo 1, conforme as placas forem se movendo, vai ficando menor, só que, nesse caso, como , e esse valor é menor do que a metade da abertura da cunha (12,5°), então a cunha irá escapar da fenda.
Passo 3
Vamos analisar agora o caso da letra em que . Conforme vimos na seção anterior do livro, o coeficiente de atrito pode ser encontrado através de:
Substituindo o valor dado de :
Então, voltando para o DCL do passo 1, conforme as placas forem se movendo, vai ficando menor, só que, nesse caso, como , conforme for ficando menor, o ângulo de contato do lado direito vai se aproximando desse valor, enquanto do outro lado teremos e a cunha ficará presa na fenda.