Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 43

Uma barra esbelta de aço de 22,5 cm de comprimento é colocada dentro de um tubo, tal como mostra a figura. Sabendo que o coeficiente de atrito estático entre a barra e o tubo é 0,20; determine o maior valor de θ para que a barra não caia dentro do tubo.

Passo 1

Tá legal! Vamos começar esse excercício desenhando o diagrama de corpo livre para a barra:

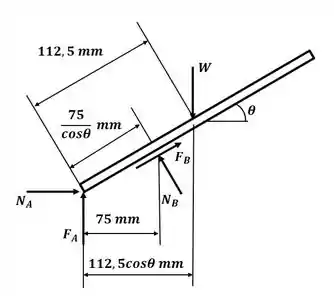
Sabemos que as forças de atrito podem ser calculadas por:

F B = μ s N B

F A = μ s N A

Agora aplicando o somatório de forças na direção x :

+ → ∑ F x = 0

N A - N B s e n θ + F B c o s θ = 0 → N A - N B s e n θ + μ s N B c o s θ = 0

N A = N B ( s e n θ - μ s c o s θ )

Essa será nossa equação 1. Agora podemos aplicar o somatório de forças na direção y :

+ ↑ ∑ F y = 0

F A + N B c o s θ + F B s e n θ - W = 0 → μ s N A + N B c o s θ + μ s N B s e n θ - W = 0

Essa será nossa equação 2.

Passo 2

Agora substituindo a equação 1 na equação 2, temos:

μ s N A + N B c o s θ + μ s N B s e n θ - W = 0

μ s N B s e n θ - μ s c o s θ + N B c o s θ + μ s N B s e n θ - W = 0

N B 1 - μ s 2 c o s θ + 2 μ s s e n θ = W → N B = W 1 - μ s 2 c o s θ + 2 μ s s e n θ

Substituindo o valor de μ s dado no enunciado, chegamos em:

N B = W 0,96 c o s θ + 0,4 s e n θ

Passo 3

Agora iremos calcular o somatório de momento em relação ao ponto A:

+ ↺ ∑ M A = 0

N B 75 c o s θ - W 112,5 c o s θ = 0

Substituindo o valor de N B encontrado no passo 2:

W 0,96 c o s θ + 0,4 s e n θ 75 c o s θ = 112,5 W c o s θ → 9,6 cos 3 ⁡ θ + 4 s e n θ cos 2 ⁡ θ - 6,67 = 0

Vamos precisar da ajuda da calculadora nessa, jogando essa equação lá, obtemos:

θ = 35,7 °

Resposta

θ = 35,7 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que o coeficiente de atrito entre o bloco de 15 kg e o plano inclinado é μ s = 0,25 , determine ( a ) o menor valor de P necessário para se manter o bloco em equilíbrio, ( b ) o valor correspo
Os coeficientes de atrito são μ s = 0,4 e μ k = 0,3 entre todas as superfícies de contato. Determine a menor força P necessária para iniciar o movimento do bloco de 30 kg se o cabo AB ( a ) está ligad
Determine o intervalo de valores de P para o qual o equilíbrio do bloco mostrado na figura é mantido.
Considerando apenas valores de θ menores que 90°, determine o menor valor de θ solicitado para o qual o movimento do bloco para a direita é iminente quando ( a ) W = 340 N, ( b ) W = 450 N.
Os coeficientes de atrito entre o bloco e o trilho são μ s = 0,3 e μ k = 0,25 . Sabendo que θ = 65 ° , determine o menor valor da força P necessária ( a ) para iniciar o movimento do bloco sobre o tri