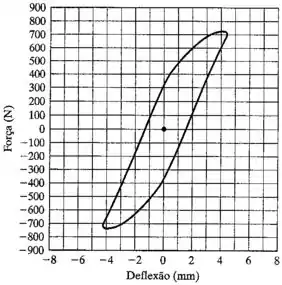
A curva experimental força-deflexão para uma estrutura composta é mostrada na Figura 2.100. Determine a constante de amortecimento por histerese, o decremento logarítmico e o fator de amortecimento viscoso equivalente correspondentes a essa curva.
Passo 1
A energia dissipada em cada ciclo de carga total é fornecida pela área delimitada pelo loop de histerese.
A área pode ser encontrada contando os quadrados incluídos no ciclo de histerese. Na Fig. 2.100, o número de quadrados é . Como cada quadrado , a energia dissipada em um ciclo é
Passo 2
Uma vez que a deflexão máxima = x = 4.3 mm, e a inclinação da curva de força-deflexão é
a constante de amortecimento de histerese é dada por