A massa de um sistema massa-mola vibra sobre uma superfície seca com uma inclinação 30 em relação à horizontal, como mostra a Figura 2.99.
- Derive a equação de movimento.
- Determine a resposta do sistema para os seguintes dadosm = 20 kg, k = 1.000 N/m, = 0,1, x0 = 0,1 m, = 5 m/s
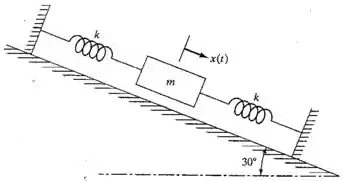
Figura 2.99
Passo 1
O exercício pede galera que a gente: Derive a equação de movimento. E determine a resposta do sistema para os seguintes dados
-
Passo 2
Caso 1:
Quando e ou e
Passo 3
Caso 2:
Quando e ou e
As Eqs. (E.1) e (E.2) podem ser escrito como uma única equação como:
Passo 2
Solução da Eq. (E.1):
Solução da Eq. (E.2):
Usando as condições iniciais em cada meio ciclo, as constantes A1 e A2 ou A3 e A4 são encontradas. Por exemplo, no primeiro meio ciclo, o movimento começa da esquerda para a direita com e . Esses valores podem ser usados na Eq. (E.4) para encontrar A1 e A2.
Resposta
Usando as condições iniciais em cada meio ciclo, as constantes A1 e A2 ou A3 e A4 são encontradas. Por exemplo, no primeiro meio ciclo, o movimento começa da esquerda para a direita com e . Esses valores podem ser usados na Eq. (E.4) para encontrar A1 e A2.