Deduza a equação de frequência para a vibracão longitudinal de uma barra escalonada que tem duas áreas de sessão transversal e ao longo dos comprimentos e , respectivamente. Considere condições de extremidade fixa-livre.
Passo 1
E aí, galerinha!
Bom! Bora lá pro que interessa!
Vamos começar fazendo um esboço do problema pra entender melhor ele...
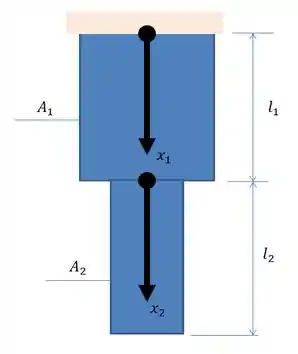
Bem! Como podemos ver aí, estamos trabalhando com duas coordenas, em e .
E as equações de movimento... Para a barra, sabemos que são dadas por...
Passo 2
Sabemos que para as condições de contorno, em , temos que...
E como a barra é escalona, temos que a condição de contorno no finalzinho da primeira barra vai ser igual à condição de contorno do início da segunda barra. Logo;
E então, ficamos com:
Isolando :
E substituindo em :
Como:
Então, ficamos com...
Uma vez que...
Dessa forma, a equação de frequência vai ser dada por...