Deduza as equações de diferenças finitas para a análise de uma membrana retangular usando m e n pontos de malha nas direções x e y, respectivamente. Considere que a membrana e fixa ao longo de todas as bordas. Use a f6rmula de diferença central.

Pelo método de separação pode ser assumido como:

Ao substituir a variável na equação (2), podemos obter:

Analisando o eixo x

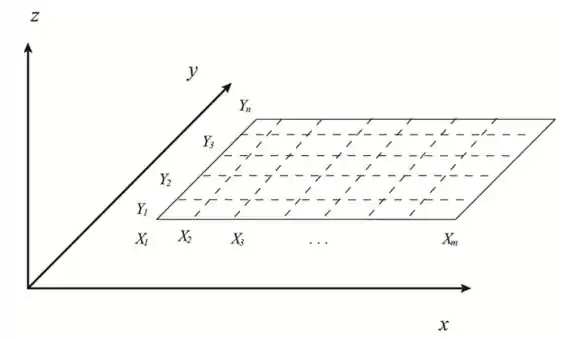
Divida o comprimento da membrana retangular na direção x em partes iguais e denote os pontos da malha como mostrado na figura a seguir. Entre cada malha tem comprimento de

A segunda derivada da equação (3) pode ser substituída pela equação de

Ao combinar as equações (3) e (6), a equação de movimento pode ser expressa da seguinte maneira:

Aplicando a equação em cada ponto da malha

Isso pode ser expresso em forma de matriz como

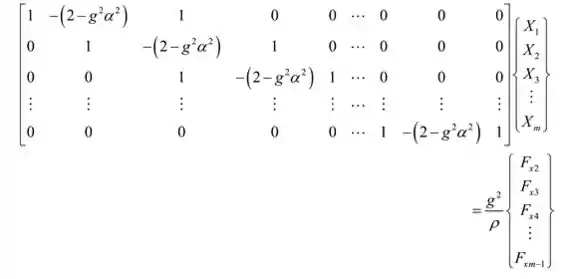
Condição de contorno

Fim fixo-fixo. O deslocamento no eixo x é zero em ambas as extremidades fixas.

Portanto, a equação da matriz pode ser reescrita como:

E obtendo a equação final

são escalares. É a ,atriz de identidade da ordem .

O problema de autovalores da equação (7) pode ser resolvido facilmente, uma vez que a matriz é uma matriz tridiagonal.

Análise no eixo y.

Divida o comprimento da membrana retangular na direção y em partes iguais e denote os pontos da malha como mostrado na figura 1. Entre cada malha tem comprimento de

A segunda derivada da equação (4) pode ser substituída pela equação de

Ao combinar as equação (4) e (8), a equação de movimento pode ser expressa como:

Aplicando a equação em cada ponto da malha .

Isso pode ser expresso em forma de matriz:

Condição de contorno

Fim fixo-fixo. O deslocamento no eixo de y é zero em ambas as extremidades fixas.

Portanto, a equação da matriz pode ser reescrita como:

E obtenha a equação final como

Com isso a matriz formada e

são escalares. É a matriz de identidade da ordem .

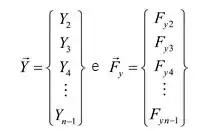
O problema de autovalores da equação (9) pode ser resolvido facilmente, uma vez que a matriz É uma matriz tridiagonal.