Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 21

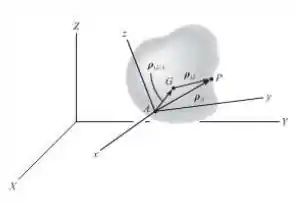
Demonstre que, se a quantidade de movimento angular de um corpo é determinada em relação a um ponto arbitrário A , então H A pode ser expresso pela equação 21.9 . Isso requer a substituição de ρ A = ρ G + ρ G / A na Equação 21.6 e expandindo, observando-se que ∫ ρ G d m = 0 por definição do centro de massa e v G = v A + ω × ρ G / A .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Por definição, temos que:

H A = ∫ m ρ A d m × v A + ∫ m ρ A × ( ω × ρ A ) d m

Desenvolvendo, temos:

H A = ∫ m ( ρ G + ρ G / A )   d m × v A + ∫ m ( ρ G + ρ G / A ) × ( ω × ( ρ G + ρ G / A ) ) d m

H A = ∫ m ρ G   d m × v A + ρ G / A × v A ∫ m d m + ∫ m ρ G × ( ω × ρ G ) d m + ∫ m ρ G d m × ω × ρ G / A + ρ G / A × ω × ∫ m ρ G d m + ρ G / A × ω × ρ G / A

Como ∫ m ρ G d m = 0 , temos que:

∫ m ρ G × ( ω × ρ G ) d m = H G

Portanto:

H A = ρ G / A × v A m + H G + ρ G / A × ω × ρ G / A m

H A = H G + ρ G / A × v A + ( ω × ρ G / A ) m

H A = H G + ( ρ G / A × m v G )

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro