Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 04

O piloto de um avião a jato avariado foi capaz de controlar seu avião reduzindo a potência dos motres. Se o avião tem uma massa de 8500 kg e um raio de giração k G = 1,41 m em relação ao centro de massa G, determine a velocidade angular do avião e a velocidade de seu centro de massa G em t = 5 s se o empuxo em cada turbina é alterado pata T 1 = 25 kN e T 2 = 4 kN, como mostrado. Originalmente o avião está voando em linha reta a 360 m/s. Despreze os efeitos de arrasto e perda de combustível.

Passo 1

Resolveremos esse exercício adotando a aceleração da gravidade g =   9,81   m / s 2 .

Inicialmente, devemos descobrir a velocidade angular no instante t = 5 s, faremos isso aplicando a equação da conservação da quantidade de movimento angular com o auxílio do esquema a seguir:

+ ↺   H G 1 + ∑ ∫ M G d t = H G 2

0 + 25000 5 0,375 - 4000 5 0,375 = 8500 1,41 2 ω

ω = 2,33   r a d / s

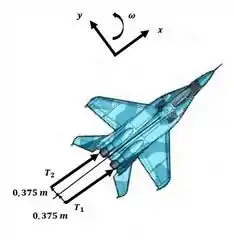
Passo 2

Agora, podemos aplicar a equação do momento linear para descobrir a velocidade do centro de massa em G no instante t = 5 s:

+ →   m v G x 1 + ∑ ∫ F x d t = m v G x 2

8500 360 + 25000 5 + 4000 5 = 8500 v G x 2

v G x 2 = 377,06   m / s

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um caixote B de 500 kg está suspenso por um cabo preso a um carrinho A de 40 kg que corre por uma viga I inclinada, tal como mostra a figura. Sabendo que no instante mostrado o carrinho tem uma aceler
Um fio único ACB de 80 cm de comprimento passa por um anel em C que está preso a uma esfera que roda com uma velocidade escalar constante v no círculo horizontal mostrado na figura. Sabendo que θ 1 =
Um caixote B de 500 kg está suspenso por um cabo preso a um carrinho A de 40 kg que corre por uma viga I inclinada, tal como mostra a figura. Sabendo que no instante mostrado o carrinho tem uma aceler
Um fio único ACB passa por um anel em C que está preso a uma esfera de 1 kg que roda com uma velocidade escalar constante v no círculo horizontal mostrado na figura. Sabendo que θ 1 = 50°, d = 0,8 m e
Uma bola presa a uma corda se move ao longo de uma trajetória circular a uma velocidade escalar constante de 4 m/s. Determine (a) o ângulo θ que a corda forma com o poste BC, (b) a tração na corda.