Derive a equação de movimento do sistema mostrado na Figura , com a utilização dos seguintes métodos:
- Segunda lei do movimento de Newton;
- Princípio de D’Alembert
- Princípio do trabalho virtual.
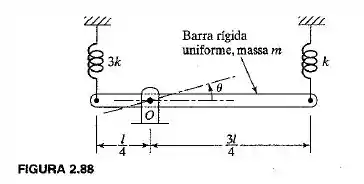
Passo 1
Oi tudo bem? Vamos analisar estes itens. O item nos pede para utilizar o método da segunda lei de Newton para a derivação.
Temos que, considerando o momento negativo no sentido horário:
Aqui o momento de inercia de massa da barra é dado por , a rigidez da mola é , o comprimento da barra é , o deslocamento angular da barra é e a aceleração angular da barra é .
Portanto a equação de movimento para o sistema de acordo com a segunda lei do movimento de Newton será:
Passo 2
Para o item vamos utilizar o princípio de D’Alembert. Temos que:
Portanto a equação de movimento para o sistema de acordo com o princípio de D’Alembert é:
Passo 3
Para o item vamos utilizar o princípio do trabalho virtual. Temos que o trabalho virtual realizado é dado por:
Sabendo que:
E que:
Temos que:
Portanto a equação de movimento para o sistema de acordo com o princípio do trabalho virtual é: