Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 2.Problemas - Ex. 82

Use o método da energia para determinar a frequência natural do sistema mostrado na Figura 2.85 .

Passo 1

Queremos a frequência natural do sistema da Figura 2.85.

Observe o seguinte diagrama para o sistema:

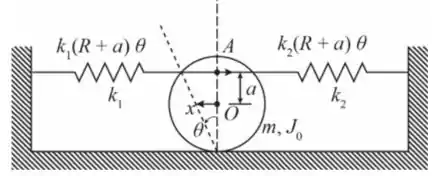
Vamos calcular a energia cinética T para o sistema:

T = 1 2 m x ˙ 2 + 1 2 J 0 θ ˙ 2

Onde x ˙ é a velocidade linear do sistema e θ ˙ a velocidade angular.

Sabendo que:

θ ˙ R = x ˙

Temos que:

T = 1 2 m θ ˙ R 2 + 1 2 J 0 θ ˙ 2

T = 1 2 m R 2 + J 0 θ ˙ 2

Temos que o momento de inércia de massa sobre o ponto O do cilindro é dado por:

J O = 1 2 m R 2

Portanto:

T = 1 2 m R 2 + 1 2 m R 2 θ ˙ 2

T = 1 2 3 2 m R 2 θ ˙ 2

T = 3 4 m R 2 θ ˙ 2

Passo 2

A energia potencial é dada por:

U = 1 2 k 1 x 1 2 + 1 2 k 2 x 1 2

Substituindo R + a θ por x 1 , temos que:

U = 1 2 k 1 R + a θ 2 + 1 2 k 2 R + a θ 2

U = 1 2 k 1 + k 2 R + a θ 2

O método da energia consiste na derivação da adição de energia cinética e potencial para se conseguir uma equação de movimento da forma:

x ¨ + ω n 2 x = 0

E é assim que encontraremos a nossa frequência natural.

Passo 3

Temos que:

d U + T d t = 0

d d t 1 2 k 1 + k 2 R + a θ 2 + 3 4 m R 2 θ ˙ 2 = 0

d d t 1 2 k 1 + k 2 R + a 2 θ 2 + d d t 3 4 m R 2 θ ˙ 2 = 0

Resolvendo, temos que:

1 2 k 1 + k 2 R + a 2 2 θ θ ˙ + 3 4 m R 2 2 θ ˙ θ ¨ = 0

Rearranjando, temos que:

1 2 k 1 + k 2 R + a 2 2 θ + 3 2 m R 2 θ ¨ = 0

3 2 m R 2 θ ¨ + k 1 + k 2 R + a 2 θ = 0

θ ¨ + k 1 + k 2 R + a 2 3 2 m R 2 θ = 0

Portanto:

ω n 2 = k 1 + k 2 R + a 2 3 2 m R 2

ω n = k 1 + k 2 R + a 2 3 2 m R 2

Resposta

ω n = k 1 + k 2 R + a 2 3 2 m R 2

Ver Outros Exercícios desse livro