Descreva o procedimento do método de diferenças finitas.
Passo 1
Fala galerinha, belezaa???
Então, o método das diferenças finitas é um método para resolver equações de derivação usando uma abordagem de aproximação. Esse método esta associado á equação diferencial governante, às condições de contorno e à substituição pelas equações de diferenças finitas correspondentes.
Passo 2
Existem três tipos de fórmulas que podem ser usadas para derivar o método das diferenças finitas. Esses são métodos de diferença para frente, para trás e central. Portanto, devemos considerar apenas o método da diferença central.
Passo 3
O procedimento do método das diferenças finitas deve ser determinado por:
- Substitua o domínio da solução por um número finito de pontos. Esses são chamados de pontos de malha ou grade. As malhas são igualmente espaçadas ao longo de cada malha. A malha divisória da solução de intervalo é apresentada na figura a seguir.
- Resolvendo a derivação de usando a expansão em série de Taylor
- Aplicando as fórmulas de derivação na equação de movimento ou outra equação que precise ser resolvida e inicie o cálculo de cada passo
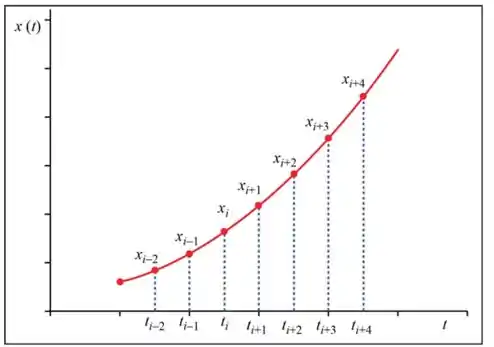
Passo 4
Ao tomar apenas dois termos e subtrair a equação (2) da equação(1), a primeira derivada de x em pode ser expressa do seguinte modo:
Levando os termos até a segunda derivada e adicionando a equação(1) e a equação (2), a segunda derivada de x em pode ser expressa do seguinte modo:
Passo 5
Por exemplo
O governo de um sistema de grau de liberdade fisicamente amortecido é
Substituindo as derivadas pela equação (3) e (4), a equação (5) pode ser reescrita como:
Por determinada condição de contorno, a equação pode ser iniciada e resolvida
Resposta
Vide o passo a passo.