Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 130

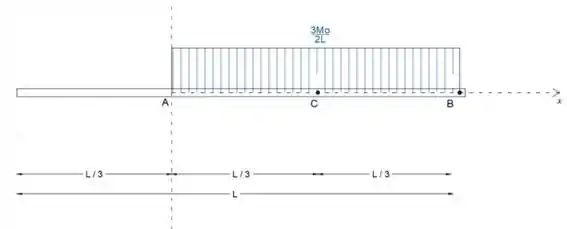
Desenhe os diagramas de cisalhamento e momento para a viga carregada. Quais são os valores de cisalhamento e momento na viga média?

Passo 1

Antes de podermos determinar a força de cisalhamento e o momento de flexão atuando, precisaremos determinar as forças de reação a partir do diagrama de corpo livre

Vamos determinar as forças de reação a partir de equações de equilíbrio

∑ M A = 0

- M 0 + Y B ⋅ 2 l 3 = 0 Y B = 3 M 0 2 l

∑ F x = 0

X A = 0

Y A - Y B = 0 Y A = Y B Y A = 3 M 0 2 l

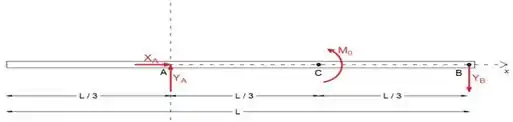
Passo 2

[ - 1 / 3 ≤ x < 0 ]

A seguir, vamos cortar e analisar a parte do feixe no intervalo [-l / 3≤x

Aplicaremos as equações de equilíbrio no diagrama de corpo livre para determinar a força de cisalhamento V e o momento fletor M. Observe que tanto V quanto M têm direção positiva (sentido)

∑ F y = 0

- V - Y A = 0 V = - Y A V 0 - 1 / 2 = - C l Diagrama de força de cisalhamento é constante nesse segmento

∑ M = 0

- Y A ⋅ x - M = 0 M = - Y A ⋅ x M 0 - 1 / 2 = - C l ⋅ x

O diagrama de momento está aumentando linearmente e seu valor no ponto ligeiramente à esquerda de C é:

M ← I 2 = - C l ⋅ l 2 = - C 2

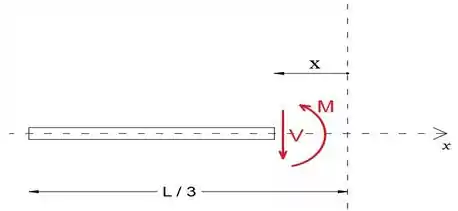
Passo 3

[ 0 ≤ x < 1 / 3 ]

A seguir, vamos cortar e analisar a parte do feixe ao longo do intervalo [0≤x

Aplicaremos as equações de equilíbrio no diagrama de corpo livre para determinar a força de cisalhamento V e o momento fletor M. Observe que tanto V quanto M têm direção positiva (sentido)

∑ F y = 0

- V + Y A = 0 V = Y A V 0 - 1 / 3 = - 3 M 0 2 l Diagrama de força de cisalhamento é constante nesse segmento

∑ M = 0

Y A ⋅ x - M = 0 M = Y A ⋅ x M 0 - 1 / 3 = - 3 M 0 2 l ⋅ x

O diagrama de momento está aumentando linearmente e seu valor no ponto ligeiramente à esquerda de C é:

M ← 1 2 = - C l ⋅ l 2 = - C 2

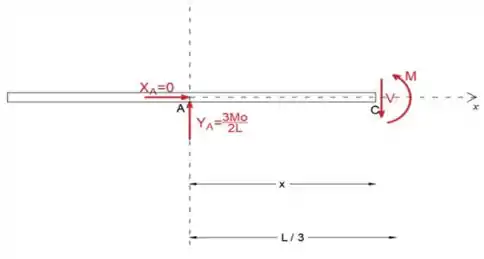
Passo 4

[ 1 / 3 < x ≤ 21 / 3 ]

A seguir, vamos cortar e analisar a parte do feixe ao longo do intervalo [l / 3

Aplicaremos as equações de equilíbrio no diagrama de corpo livre para determinar a força de cisalhamento V e o momento fletor M. Observe que tanto V quanto M têm direção positiva (sentido)

∑ F y = 0

V - Y B = 0 V = Y B V 1 / 3 - 21 / 3 = 3 M 0 21 Diagrama de força de cisalhamento é constante nesse segmento

∑ M = 0

Y B ⋅ 2 l 3 - x + M = 0 M = - Y B 2 l 3 - x M 1 / 3 - 21 / 3 = - 3 M 0 21 ⋅ 21 3 - x

O diagrama de momento está aumentando linearmente e seu valor no ponto ligeiramente à esquerda de C é:

M → 1 3 = - 3 M 0 2 l ⋅ 2 l 3 - l 3 = - M 0 2

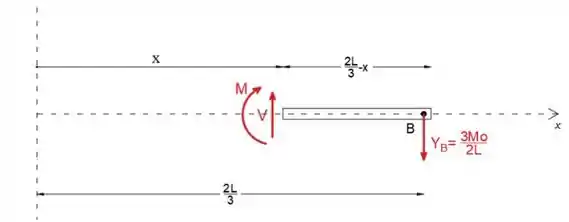
Passo 5

Faremos um gráfico das funções de força de cisalhamento para obter a força de cisalhamento

Passo 6

Vamos representar graficamente a função do momento fletor para obter o diagrama do momento fletor

Resposta

V l / 2 = - C L

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Localize o centro de massa z - do sólido consistindo em um núcleo central cilíndrico A , com densidade de 7,90M g / m 3 , uma parte externa cilíndrica B e um cone C no topo, cada um desses dois último
Um furo com raio r deve ser feito no centro do bloco homogêneo. Determine a profundidade h do furo de modo que o centro de gravidade G seja o mais baixo possível.
Determine a profundidade h do furo de 100m m de diâmetro feito na base do cone de modo que o centro de massa do sólido resultante esteja localizado em z -=115m m . O material tem densidade de 8M g / m
A placa composta é feita de segmentos de aço ( A ) e latão ( B ) . Determine a massa e a localização ( x - ,y - ,z - ) de seu centro de massa G . Considere ρ a ç o = 7,85M g / m 3 ç e ρ l a t ã o = 8,
Determine a distância z - até o centroide do sólido que consiste em um cone com um furo de altura h=50m m feito em sua base.