Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 107
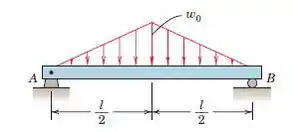
Determine as reações nos apoios A e B para a viga carregada como mostrado.
Passo 1
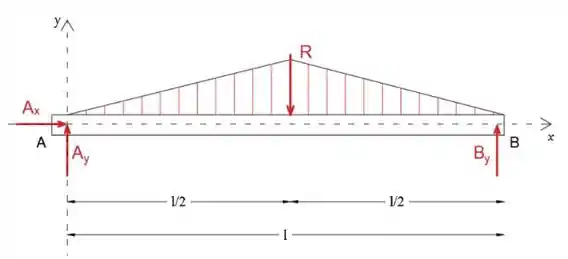
Primeiro, vamos isolar e desenhar o diagrama de corpo livre da viga
Observe que substituímos a carga distribuída por sua resultante que atua em seu centroide (no meio da viga)
Uma vez que a carga distribuída é feita de duas cargas triangulares de comprimento l / 2 e altura , podemos escrever a resultante como:
Passo 2
Ao igualar a soma das forças na direção x a zero, podemos determinar a força de reação Ax
Observe que tanto a estrutura quanto o carregamento são simétricos, portanto, as forças de reação em A e B devem ser iguais
E ao igualar a soma das forças na direção y a zero, podemos determiná-las.
Substitua R por
Uma vez que as forças de reação em A e B são iguais, podemos escrever a força By como: