Enunciado
Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 1.Problemas - Ex. 38
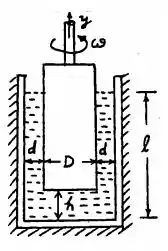
Desenvolva uma expressão para a constante de amortecimento de um amortecedor rotacional mostrado na Figura 1.83 em termos de e , onde denota a velocidade angular constante do cilindro interno e e representa as folgas radial e axial entre os cilindros interno e externo.
Passo 1
Opa galerinha, beleza com vocês?! Então bora lá pra cima dessa questão! Da formula padrão para a velocidade tangencial de um cilindro, temos que:
Para um valor de pequeno, temos essa taxa de mudança na velocidade do fluido:
E a tensão de cisalhamento entre os cilindros é dada por:
A força de cisalhamento é:
E por fim, o torque desenvolvido é:
Passo 2
Agora que temos as formulas que vamos usar na questão, vamos por a mão na massa! Para um pequeno, a taxa de mudança de velocidade do fluido em uma direção vertical é:
Tensão de cisalhamento para esse caso:
Força em uma área .
Passo 3
A partir disso, o torque entre as superfícies inferiores do cilindro é dada por:
Onde,
Logo,
Portanto, o torque final é dado por:
Passo 4
Expressando como v:
Temos uma constante de amortecimento: