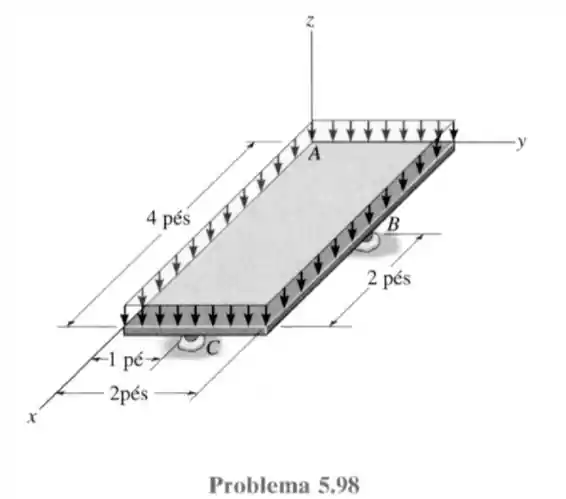
98- Determine os componentes de reação nos apoios esféricos e na junta esférica (não mostrada na figura) para a placa carregada uniformemente.
Passo 1
Por ser uma carga uniforme podemos colocar o peso total sendo a área da placa multiplicado pela carga que vamos chamar de . Logo essa carga valerá:
Assim temos o seguinte sistema de forças.
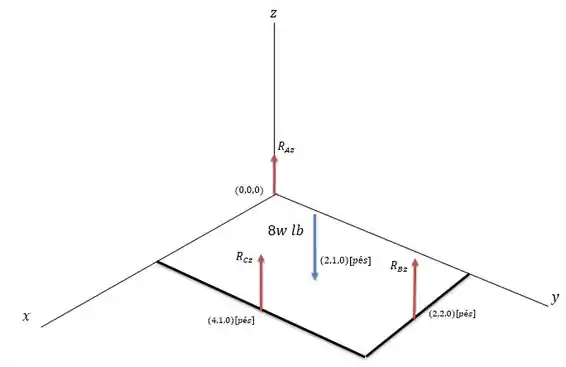
Como não temos forças horizontais então as reações em e na junta serão zero. Ou seja:
Passo 2
A somatória das forças verticais nos dá:
Fazendo a somatória dos momentos no eixo nós temos (considerando sentido anti-horário como negativo).
Passo 3
Agora fazendo a somatória dos momentos no eixo temos:
Fazendo um sistema dessa equação com a última do passo nos dá as seguintes reações:
E se aplicarmos esse resultado na equação:
Nós encontraremos:
Resposta
Acreditamos que a questão simplesmente esqueceu de informar o valor de .