Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas Fundamentais - Ex. 20

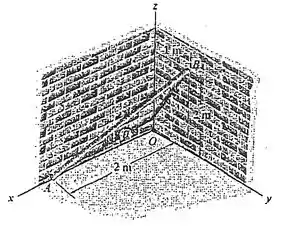
Determine o comprimento da barra e o vetor posição direcionado de A a B . Qual é o ângulo θ .

Passo 1

Encontraremos o comprimento da barra através do módulo do nosso vetor. Vamos começar definindo as coordenadas dos pontos de início e fim:

A 2 ,   0 ,   0   m

B 0 ,   1 ,   2   m

E achamos nosso vetor direcionado de A a B pela subtração entre os pontos final e inicial com seus devidos vetores unitários:

r A B = { 0 - 2 i + 1 - ( 0 ) j + 2 - 0 k }

r A B = - 2 i + 1 j + 2 k   m

Passo 2

Com isso, podemos encontrar a intensidade do vetor, o comprimento da barra:

r A B = - 2 2 + 1 2 + 2 2

r A B = 3   m

Passo 3

O ângulo θ que queremos é 180 ° menos o ângulo α que nosso vetor faz com eixo x , assim:

α = cos - 1 ⁡ - 2 3 ∴ α = 131,8 °

E nosso ângulo:

θ = 180 ° - 131,8 ° ∴ θ = 48,2 °

Resposta

r A B = 3   m

r A B = - 2 i + 1 j + 2 k   m

θ = 48,2 °

Ver Outros Exercícios desse livro