Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 50
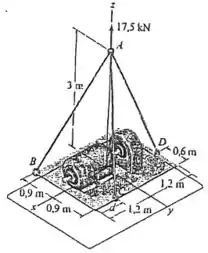
Determine a força em cada cabo para suportar a plataforma de 17,5 kN (). Considere .
Passo 1
Fala aii galerinha bonita do RespondeAí, tudo beleza?! Bora lá fazer esse exercício aqui!
O enunciado nos disse que temos uma plataforma sendo suportada através de cabos como na figra abaixo:
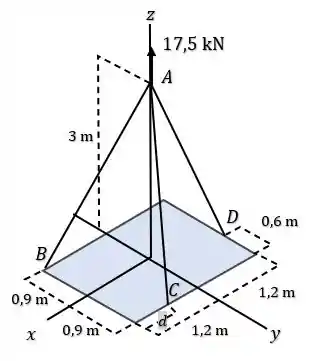
E sabendo disso, o enunciado quer que a gente encontre a força em cada cabo necessária para suportar esse peso da plataforma.
Mas calma lá meu patrão, vamos com com carinho que vai dar certo!
Antes de mais nada, devemos desenhar o diagrama de corpo livre, com essas forças em cada cabo, de maneira que fique mais ou menos assim:
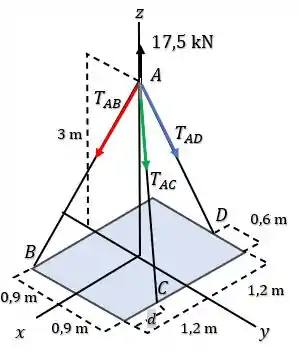
Isso é bom, porque agora sabemos que a força está na direção do vetor , da mesma maneira a força está na direção e na direção .
Passo 2
Iradoso, então se a gente conseguir expressar o vetor unitário de cada uma dessas direções, vamos poder expressar a forma vetorial das forças através da equação:
Então por exemplo para a força , sabemos que seu vetor diretor é , dado como:
Onde é o ponto e é o ponto , tal que:
Então pra gente encontrar o vetor unitário desse vetor diretor, é só a gente dividir ele pelo módulo dele mesmo:
Logo:
Então podemos escrever como:
Ou então:
Passo 3
Iradoso, agora se a gente fizer o mesmo para , vamos ter que:
Como o enunciado nos deu que , então:
Então o vetor unitário será:
Sendo assim, será dada como:
Passo 4
E decompondo a ultima força vamos obter que:
Logo:
Sendo assim:
Então a forma vetorial de será:
Tá ficando bonito.
Passo 5
Como a plataforma esta em equilíbrio, isso requer quer que o somatório de forças em cada dimensão seja nulo, ou seja:
E como a gente já escreveu as forças e suas componentes de cada eixo, vai ficar bonitinho pra gente escrever esses somatórios.
Então primeiro para o eixo , vamos ter que
Para o eixo :
E agora para com o eixo :
Passo 6
Belezoca, e com isso a gente conseguiu montar um sisteminha de equações e variavies dado como:
E resolvendo esse sistema linear, vamos descobrir que:
