Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas Fundamentais - Ex. 16
Expresse a força como um vetor cartesiano.
Passo 1
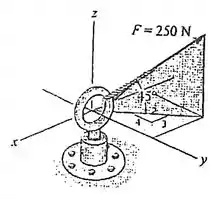
Vamos encontrar as componentes da força nos eixos
O ângulo 45 é feito entre o plano e nossa , preste atenção que aqui o cateto oposto é nossa componente em , então já vamos acha-la:
Enquanto isso, no cateto adjacente temos a componente :
Agora projetada no plano nossa componente pode ser separada em e em , já que nos é fornecida a relação por um triângulo de lados 3-4-5, ficamos com:
Passo 2
Por fim, escrevendo nossa força como vetor cartesiano:
Repare que a direção é negativa pois a componente aponta no sentido oposto do crescimento de .