Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 1.Problemas - Ex. 9

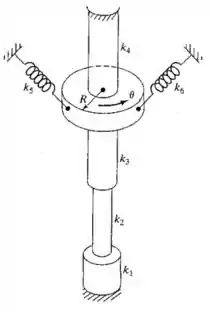
Determine a constante elástica torcional equivalente do sistema mostrado na Figura 1.61. Admita que k 1 , k 2 , k 3 e k 4 são constantes torcionais e que k 5 e k 6 são constantes elásticas lineares.

Passo 1

Opa, vamo que vamo pra essa questão? Ela nos entrega um sistema com dois tipos de constantes elásticas. Uma torcional e uma linear. A torcional a primeiro momento pode parecer ruim e difícil ela estar aí, porem a questão nos entrega o sentido do movimento θ , que é circular então fica tudo tranquilo. Bora ir atrás dessas constantes equivalentes?!

Passo 2

Vamos começar com as torcionais k 1 , k 2 e k 3 . Nela temos que:

1 k 123 = 1 k 1 + 1 k 2 + 1 k 3

Logo:

k 123 = k 1 k 2 k 3 k 1 k 2 + k 2 k 3 + k 1 k 3

Passo 3

Para as outras equivalências vamos aplicar a mesma fórmula para torções e molas. Temos que:

1 2 k e q θ 2 = 1 2 k 4 θ 2 + 1 2 k 123 θ 2 + 1 2 k 5 θ R 2 + 1 2 k 6 θ R 2

Dando aquela simplificada que a gente gosta:

k e q = k 4 + k 123 + R 2 k 5 + R 2 k 6

Logo:

k e q = k 4 + k 1 k 2 k 3 k 1 k 2 + k 2 k 3 + k 1 k 3 + R 2 ( k 5 + k 6 )

Resposta

k e q = k 4 + k 1 k 2 k 3 k 1 k 2 + k 2 k 3 + k 1 k 3 + R 2 ( k 5 + k 6 )

Ver Outros Exercícios desse livro