Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 63

Determine a coordenada x do centroide do sólido mostrado na figura. (Dica: a altura y do sólido é proporcional à coordenada x ; faça uma analogia entre essa altura e a pressão da água sobre uma superfície submersa.)

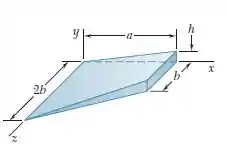
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos pegar um elemento como mostrado na figura:

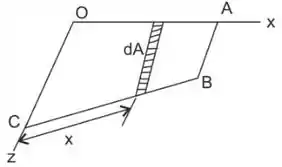
Vamos calcular o volume da faixa elementar:

d V = y d A

Sabemos que:

y = h a x

Vamos então calcular a coordenada x do centroide:

x - = ∫ x d V ∫ d V

Substituindo, temos que:

x - = ∫ x y d A ∫ y d A

x - = ∫ x h a x d A ∫ h a x d A

x - = ∫ x h a x d A ∫ h a x d A

x - = ∫ x 2 d A ∫ x d A

Podemos representar como:

x - = I z A x - A A

Passo 2

Agora imagine a seguinte divisão:

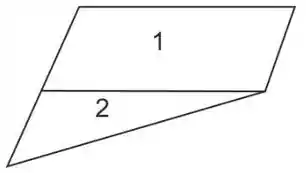
Vamos calcular os momentos de inércia da áreas:

I z A = I z A 1 + I z A 2

I z A = b a 3 12 + b a 3 3

I z A = 5 b a 3 12

Podemos então calcular o valor de x - A para a área O A B C .

x - A A = ∑ x - A

x - A A = a 2 a b + a b 2 a 3

x - A A = 4 a 2 b 6

Passo 3

Vamos calcular o centroide do volume:

x - = I z A x - A A

Substituindo, temos:

x - = 5 b a 3 12 4 a 2 b 6

x - = 5 a b 8

Resposta

x - = 5 a b 8

Ver Outros Exercícios desse livro