Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 64

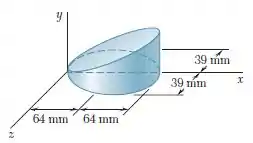
Determine a coordenada x do centroide do sólido mostrado; esse sólido foi obtido pela interseção de um cilindor elíptico com um plano oblíquo. (Veja a dica do problema 9.63 )

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Temos que:

y = h a x

Vamos então calcular a coordenada x do centroide:

x - = ∫ x d V ∫ d V

Substituindo, temos que:

x - = ∫ x y d A ∫ y d A

x - = ∫ x h a x d A ∫ h a x d A

x - = ∫ x h a x d A ∫ h a x d A

x - = ∫ x 2 d A ∫ x d A

Podemos representar como:

x - = I z x - A

Passo 2

Para o volume fornecido, temos que:

I z = π 4 39 64 2 + π 39 64 64 2

I z = 40,15 × 10 6   m m 4

E:

x - A = 64 π 39 64

x - A = 0,502 × 10 6 m m 3

Substituindo os valores, temos que:

x - = 40,15 × 10 6   0,502 × 10 6

x - = 79,98   m m

Resposta

x - = 79,98   m m

Ver Outros Exercícios desse livro