Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 71

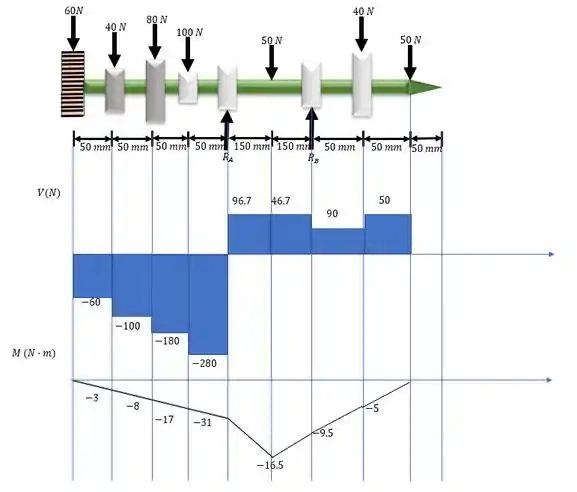
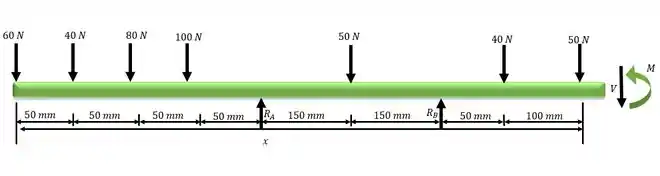
Determine os diagramas de esforço cortante e de momento fletor para o eixo de um torno se ele estiver sujeito às cargas mostradas. O mancal em A é um mancal radial, e em B é um nacal axial.

Passo 1

Desenhando o diagrama do corpo livre:

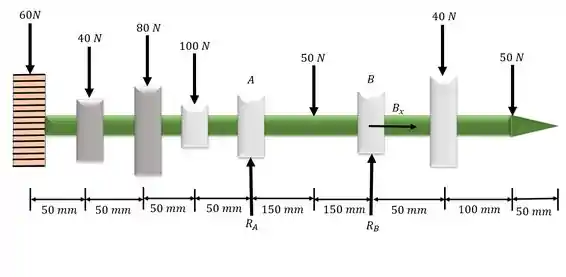
Passo 2

Com o diagrama do corpo livre traçado, podemos calcular as reações de apoio: Σ F y = 0 R A + R B = 60 + 40 + 80 + 100 + 50 + 40 + 50 R A + R B = 420 R B = 420 - R A

Σ F x = 0 B x = 0 Σ M B = 0 40 × 0,05 + 50 × 0,150 - 50 × 0,150 - R A × 0,300 - 100 × 0,350 - 80 × 0,400 - 40 × 0,450 - 60 × 0,500 = 0 0,300 R A = 113 R A = 376,66   N ⇒ R B = 43,33   N

Passo 3

Fazendo a análise do cortante e momento fletor para o trecho 0 ≤ x < 50   m m :

Σ F y = 0

V + 60 = 0 V = - 60   N

Em relação ao ponto seccionado:

Σ M = 0 M + 60 x = 0 M = - 60 x

Passo 4

Fazendo a análise do cortante e momento fletor para o trecho 50 ≤ x < 100   m m :

Σ F y = 0

V + 60 + 40 = 0 V = - 100   N

Em relação ao ponto seccionado:

Σ M = 0 M + 60 x + 40 x - 0,050 = 0 M + 60 x + 40 x - 2 = 0 M = - 100 x + 2

Passo 5

Fazendo a análise do cortante e momento fletor para o trecho 50 ≤ x < 1 50   m m :

Σ F y = 0

V + 60 + 40 + 80 = 0 V = - 180   N

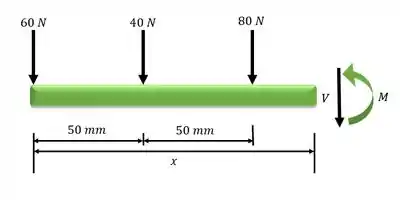
Em relação ao ponto seccionado:

Σ M = 0 M + 60 x + 40 x - 0,050 + 80 ( x - 0,1 ) = 0 M + 60 x + 40 x - 2 + 80 x - 8 = 0 M = - 180 x + 10

Passo 6

Fazendo a análise do cortante e momento fletor para o trecho 150 ≤ x < 200   m m :

Σ F y = 0

V + 60 + 40 + 80 + 100 = 0 V = - 280   N

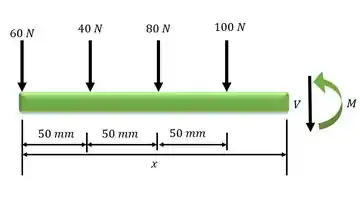
Em relação ao ponto seccionado:

Σ M = 0 M + 60 x + 40 x - 0,050 + 80 x - 0,1 + 100 ( x - 0,15 ) = 0 M + 60 x + 40 x - 2 + 80 x - 8 + 100 x - 15 = 0 M = - 280 x + 25

Passo 7

Fazendo a análise do cortante e momento fletor para o trecho 200 ≤ x < 350   m m :

Σ F y = 0

V + 60 + 40 + 80 + 100 - 376,66 = 0 V = - 96,66

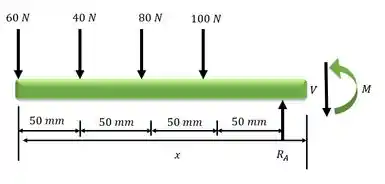
Em relação ao ponto seccionado:

Σ M = 0 M + 60 x + 40 x - 0,050 + 80 x - 0,1 + 100 x - 0,15 - 376,66 ( x - 0,2 ) = 0 M + 60 x + 40 x - 2 + 80 x - 8 + 100 x - 15 - 376,66 x + 75,33 = 0 M = 96 , 66 x - 50,33

Passo 8

Fazendo a análise do cortante e momento fletor para o trecho 350 ≤ x < 500   m m :

Σ F y = 0

V + 60 + 40 + 80 + 100 - 376,66 + 50 = 0 V = 46,66

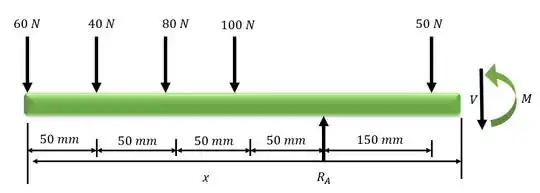
Em relação ao ponto seccionado:

Σ M = 0 M + 60 x + 40 x - 0,050 + 80 x - 0,1 + 100 x - 0,15 - 376,66 x - 0,2 + 50 ( x - 0,35 ) = 0 M + 60 x + 40 x - 2 + 80 x - 8 + 100 x - 15 - 376,66 x + 75,33 + 50 x - 17,5 = 0 M = 46,66 x - 32,83

Passo 9

Fazendo a análise do cortante e momento fletor para o trecho 500 ≤ x < 5 5 0   m m :

Σ F y = 0

V + 60 + 40 + 80 + 100 - 376,66 + 50 - 43,33 = 0 V = - 89,99

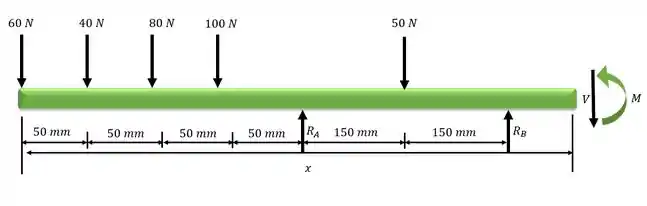
Em relação ao ponto seccionado:

Σ M = 0 M + 60 x + 40 x - 0,05 0 + 80 x - 0,1 + 100 x - 0,15 - 376,66 x - 0,2 + 50 x - 0,35 - 43,33 x - 0,5 = 0 M + 60 x + 40 x - 2 + 80 x - 8 + 100 x - 15 - 376,66 x + 75,33 + 50 x - 17,5 - 43,33 x + 21,67 = 0 M = - 89,99 x - 54,5

Passo 10

Fazendo a análise do cortante e momento fletor para o trecho 500 ≤ x < 6 50   m m :

Σ F y = 0

V + 60 + 40 + 80 + 100 - 376,66 + 50 - 43,33 + 40 = 0 V = - 4 9,99

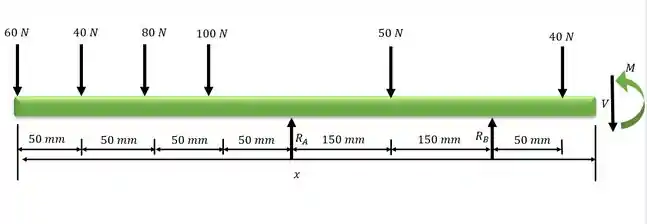
Em relação ao ponto seccionado:

Σ M = 0 M + 60 x + 40 x - 0,050 + 80 x - 0,1 + 100 x - 0,15 - 376,66 x - 0,2 + 50 x - 0,35 - 43,33 x - 0,5 + 40 x - 0,55 = 0 M + 60 x + 40 x - 2 + 80 x - 8 + 100 x - 15 - 376,66 x + 75,33 + 50 x - 17,5 - 43,33 x + 21,67 + 40 x - 22 = 0 M = - 4 9,99 x - 32,5

Passo 11

Fazendo a análise do cortante e momento fletor para o trecho 650 ≤ x < 700   m m :

Σ F y = 0

V + 60 + 40 + 80 + 100 - 376,66 + 50 - 43,33 + 40 + 50 = 0 V = 0

Em relação ao ponto seccionado:

Σ M = 0 M + 60 x + 40 x - 0,050 + 80 x - 0,1 + 100 x - 0,15 - 376,66 x - 0,2 + 50 x - 0,35 - 43,33 x - 0,5 + 40 x - 0,55 + 50 × ( x - 0,65 ) = 0 M + 60 x + 40 x - 2 + 80 x - 8 + 100 x - 15 - 376,66 x + 75,33 + 50 x - 17,5 - 43,33 x + 21,67 + 40 x - 22 + 50 × x - 32,5 = 0 M = 0

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os diagramas de esforço cortante e de momento fletor para a viga.
Determine os diagramas de esforço cortante e de momento fletor para a viga.
Determine a maior intensidade w 0 da carga distribuída que a viga pode suportar se a viga suporta uma força cortante máxima V m á x = 6k N á e um momento fletor máximo M m á x = 1k N ∙ m á .
Determine os diagramas de esforço cortante e de momento fletor para a viga com extremidade em balanço.
Determine os diagramas de esforço cortante e de momento fletor para a viga C D .