Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 68
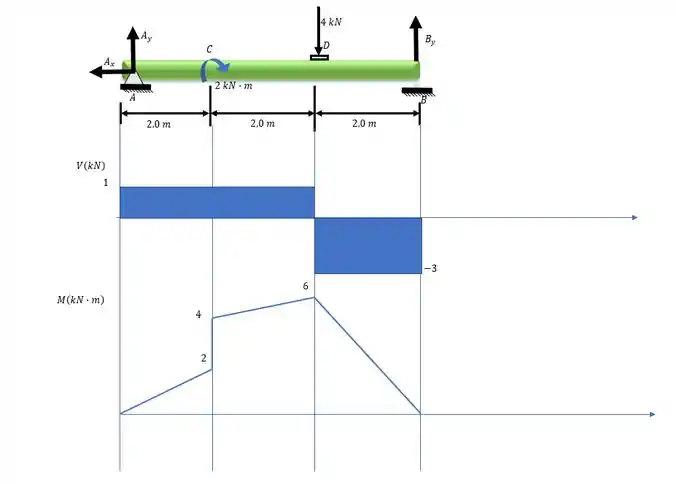
Determine os diagramas de esforço cortante e de momento fletor para a viga simplesmente apoiada.
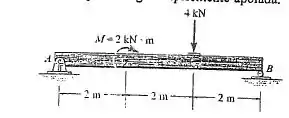
Passo 1
Falaaa, querido! Aqui ele quer os diagramas de momento e cortante.
Para determinar os diagramas de esforço, em primeiro lugar as reações de apoio devem ser determinadas.
Há algumas formas de fazer os diagramas depois desse passo. Uma delas é achando as equações desses esforços. A outra é utilizado métodos gráficos. Como o capítulo dessa questão trata de métodos gráficos, é isso que a gente vai usar, ok?
Desenhando o diagrama do corpo livre:
Passo 2
Com o diagrama do corpo livre traçado, podemos calcular as reações de apoio:
Fazendo o somatório de momentos em :
Passo 3
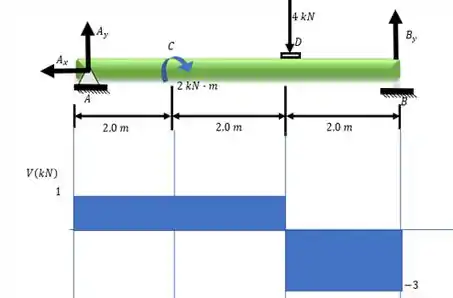
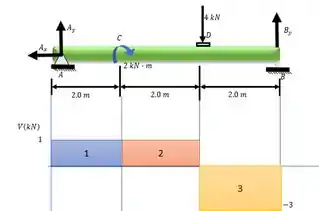
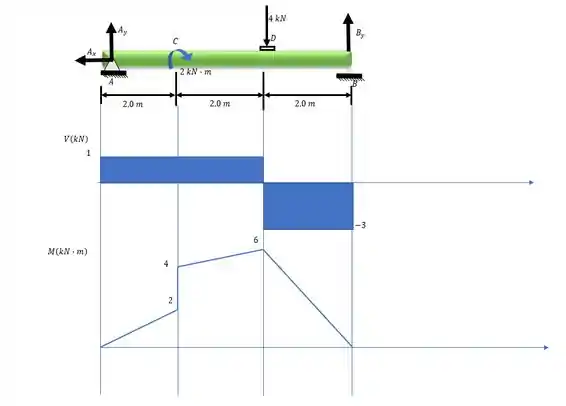
Partiu fazer o diagrama de esforços cortante pelo método gráfico. Como funciona?
Cara, primeiro a gente vai ignorar o momento concentrado aqui. Fingir que ele nem existe. Aí vamos olhar para nossas cargas e seguir o sentido (e intensidade) que elas tiverem.
Começando lá no ponto , temos a reação que é uma força concentrada e vale . Aí no nosso diagrama a gente sai de e sobe (sentido da força) verticalmente , depois, permanece constante até esbarrar em um ponto onde há outra carga concentrada.
Chegamos na carga de para baixo. Então a gente desce nesse ponto e fica constante até o ponto , onde a gente sobre . E assim, voltamos a .
Depois dessa jornada, nosso diagrama ficou assim:
Passo 4
Também podemos usar um método gráfico para o momento fletor. A ideia é que o momento em cada ponto é a soma algébrica da área no diagrama cortante.
Só temos que tomar cuidado com o momento concentrado. No ponto que ele está, como ele está no sentido horário, há um pulo para cima no diagrama. Então a partir desse ponto, os momentos serão a soma algébrica das áreas do diagrama cortante até o ponto em questão mais esse momento.
Vamos calcular as áreas. Lembra que agora o momento é um ponto importante, por isso a gente calcula área antes e depois dele.
Aí os momentos ficam:
A partir de , a gente adiciona o momento concentrado, aí a gente precisa calcular esse ponto com o momento e um ponto auxiliar sem o momento.
Entre as cargas pontuais, ligamos esses pontos por retas.
Fica assim:
Resposta
