Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 72
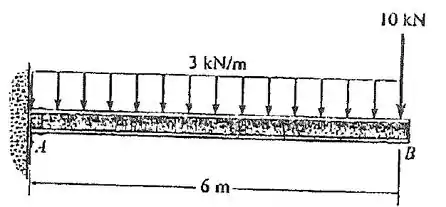
Determine os diagramas de esforço cortante e de momento fletor para a viga.
Passo 1
Fala!
O problema quer que a gente encontre o diagrma do esforço cortante e o momento fletor na viga. Nesse tipo de questão a gente segue um passo a passo maneiro e dá bom!
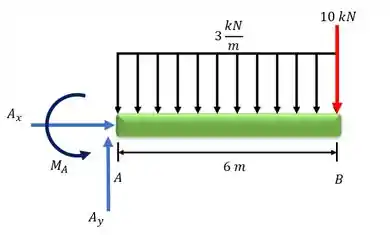
Vamos começar calculando as reações no ponto . Desenhando o diagrama do corpo livre:
Vamos!
Passo 2
Com o diagrama do corpo livre traçado, podemos calcular as reações de apoio:
Falta só a gente achar a reação do momento em . Vamos considerar o sentido anti-horário positivo. Lembrando que a resultante do carregamento positivo fica na metade dele. Ficamos assim:
Passo 3
Cara, para achar os diagramas, podemos achar as equações de e . Mas esse capítulo trata de como fazer esses carinhas pelos métodos gráficos. Então o que a gente vai fazer é usar um método gráfico. Uhul!
Como ele funciona para o cortante? Vou te mostrar. Temos essa viga:
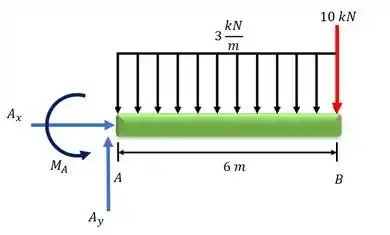
A ideia é a gente seguir essas setinhas para desenhar nosso diagrama..
Fica assim:
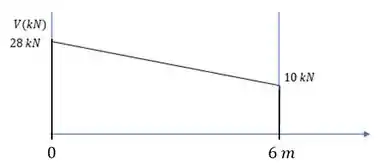
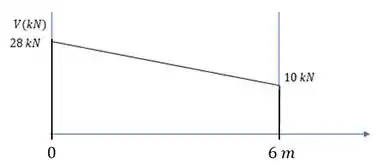
Como a gente fez: Vamos seguir as setinhas do nosso DCL. Em subimos(sentido da força) . E nesse ponto já começa a carga distruibuida de .
Aí a gente faz uma reta descendo com inclinação de (a partir do ponto onde paramos em , depois de subir por causa de ) até chegar no ponto , onde o carregamento distrubuído acaba. Você pode reparar que descemos o valor da resultante do carregamento, mas como uma reta inclinada.
Depois, encontramos outra carga concetrada, a de para baixo. O que faz? Pula para baixo de onde a gente estava.
Para confirmar se está certo, esse final tem que ser zero. Como ficou ali na nossa 😊
Passo 4
Também podemos usar um método gráfico para o momento fletor. A ideia é que o momento em cada ponto é a soma algébrica da área no diagrama cortante.
Maaas, repara que temos o momento concetrado que é a reação em . Nele, nosso diagrama dá um salto para baixo, isso porque o momento está no sentido anti-horário.
Já que ele está no começo da viga, nosso momento em , já começa como
Agora sim, vamos calcular as áreas.
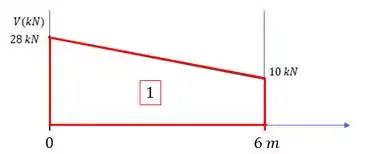
Só temos uma área que é a área de um trapézio, então fazemos
Aí os momentos ficam:
Para calcular os momentos nos pontos que ficam depois do momento concentrado, a gente precisa adcionar o valor do momento, então fica
Já que entre e temos um carregamento distribuído com constante, nós ligamos os pontos por uma parábola, com concavidade para baixo, já que nesse intervalo é descrescente.
E já que o cortante não zera, nosso momento não tem máximos ou mínimos locais (carinha de monte ou de vale).
Fica assim nosso diagrama:
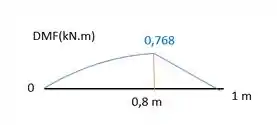
Como em , a gente sabe que o ponto máximo do momento não está no intervalo da parábola, mas em . Então o desenho está certinho!
Resposta
