Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 2.Problemas - Ex. 74

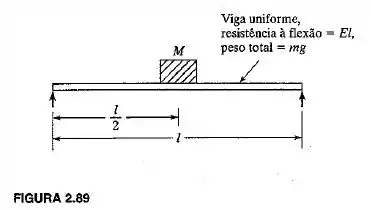
Determine o efeito do peso próprio sobre a frequência natural de vibração da viga fixa nas duas extremidades (Figura 2.89 ).

Passo 1

Oi, tudo bem? Vamos analisar esta questão.

Primeiro vamos calcular a deflexão y x da viga à distância x :

y x = y 0 3 x l - 4 x 3 l 3

Podemos observar que a deflexão máxima será y 0 .

A energia cinética máxima devido à massa distribuída, será:

T = 2 1 2 m l ∫ 0 l 2 y ˙ 2 x , t ​ m á x d x + 1 2 y ˙ m á x 2 M

Onde M representa a massa ligada ao feixe. Desenvolvendo, temos que:

T = 2 1 2 m l ∫ 0 l 2 ω n y x 2 d x + 1 2 ω n y 0 2 M

T = m ω n 2 y 0 2 l ∫ 0 l / 2 ω n y 0 3 x l - 4 x 3 l 3 2 d x + 1 2 ω n y 0 2 M

Resolvendo a integral, temos que:

T = m ω n 2 y 0 2 l 3 x 3 l 2 + 16 x 7 7 l 6 - 24 x 5 5 l 4 0 l / 2 + 1 2 ω n y 0 2 M

T = 1 2 ω n 2 y 0 2 17 35 m + M

A parte efetiva da massa da equação de energia que encontramos é de:

m e f = 17 35 m

Sendo esta a parte efetiva do peso próprio do feixe na energia cinética.

m e f = 0,4857 m

Resposta

m e f = 0,4857 m

Ver Outros Exercícios desse livro