Determine a equação de movimento diferencial para o sistema vibratório amortecido mostrado. Que tipo de movimento ocorre? Tome , , .
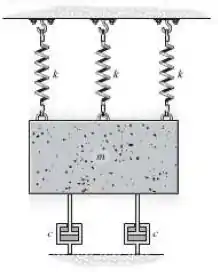
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Analisando verticalmente, temos que:
Substituindo os valores, temos:
Simplificando, temos:
Comparando com a EDO padrão, temos que:
Logo:
Temos que:
Para o nosso problema,
Por definição . Portanto:
Como , temos que o sistema é superamortecido.
Resposta
Como , temos que o sistema é superamortecido.