Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 33

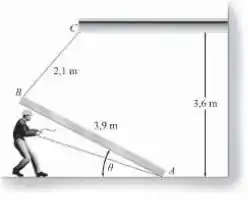
A viga tem uma massa de 750   k g e está sendo levantada para uma posição vertical puxando-se muito devagar sua extremidade inferior A . Se a corda arrebenta quando θ = 60 ° , e a viga está essencialmente em repouso, determine a velocidade de A no instante que a corda B C torna-se vertical. Despreze o atrito e a massa das cordas e trate a viga como uma barra fina.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Podemos aplicar o princípio do trabalho e energia analisando o momento incial e final do sistema para encontrar a velocidade do ponto A .

T 1 + ∑ U 1 → 2 = T 2

T 1 = 1 2 m v 1 2

Como o sistema está em repouso no momento inicial, temos que v 1 é nulo, logo:

T 1 = 0

Note que a energia cinética inicial T 1 = 0 porque, imediatamente após a corda quebrar, a viga fica momentaneamente em repouso antes de começar a deslizar no chão.

Podemos considerar também que na posição final ω = 0 e o objeto está em translação pura.

Para o momento final, temos:

T 2 = 1 2 m v 2 2

Sendo v 2 a velocidade do centro de massa no final do movimento analisado.

Temos então que:

T 2 = 1 2 750 v G 2

T 2 = 375 v G 2

Passo 2

A parcela do trabalho ∑ U 1 → 2 , será:

∑ U 1 → 2 = m g h 1 - m g h 2

Fiz esses diagramas para descobrirmos os valores de h 1 e h 2 .

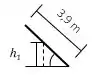
O tamanho h 2 é bem simples de ser encontrado, pois é o momento em que a corda B C está reta na vertical.

h 2 = 3,6 - 2,1 2

h 2 = 0,75   m

Para encontrar h 1 temos que o ângulo inicial é de θ = 60 ° , logo:

h 1 = 3,9 2 sin ⁡ 60 °

h 1 = 1,689   m

Lembrando que h 1 e h 2 são as alturas iniciais e finais do centro de massa.

Portanto:

∑ U 1 → 2 = m g ( h 1 - h 2 )

∑ U 1 → 2 = 750 9,81 1,689 - 0,75

∑ U 1 → 2 = 6906,85

Agora é só aplicar:

T 1 + ∑ U 1 → 2 = T 2

0 + 6906,85   = 375 v G 2

v G = v A = 4,3   m / s

Resposta

v G = v A = 4,3   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O vetor posição de uma partícula é dado por r = 8 ti + 1,2 t 2j - 0,5 t 3 - 1k , onde t é o tempo em segundos a partir do início do movimento e onde r é expresso em metros. Para a condição em que t =
O homem e sua bicicleta têm uma massa combinada de 95k g . Que potência P o homem desenvolve subindo a inclinação de 5 % a uma velocidade constante de 20k m / h ?
O carrinho tem uma velocidade v A = 4m / s quando passa pelo ponto A . Este se desloca sem atrito considerável e passa sobre o topo da elevação da pista. Determine a velocidade do carrinho quando este
O cursor C de 0,5k g parte do repouso em A e desliza com atrito desprezível sobre a haste fixa no plano vertical. Determine a velocidade v com que o cursor golpeia a extremidade B quando atuado por um
Utilize como referência a figura do Prob. 3/105. Sabe-se que o carrinho de 3k g passa sobre o topo da pista e chega em B com uma velocidade v B = 6m / s , determine o trabalho realizado pelo atrito en