Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas fundamentais - Ex. 2
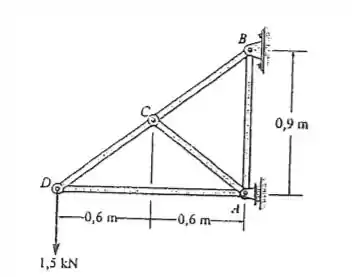
Determine a força em cada membro da treliça. Indique se os membros estão sob tração ou compressão.
Passo 1
Desejamos encontrar as forças em cada membro da treliça e, para isso, vamos utilizar o seguinte diagrama de corpo livre
Primeiramente vamos levar em conta as seguintes considerações: como regra geral, se somente duas barras não colineares se ligam em um nó, então, ambas são barras de força nula. Além disse, se três barras se unem num nó para o qual duas delas são colineares e nenhuma força externa é aplicada nesse nó, então, a terceira barra é de força nula. Isso implica que .
Agora, calculando as reações de apoio vamos ter
Adotando o sentido anti-horário como positivo vamos ter
Passo 2
Agora analisaremos cada nó por vez de tal forma que consigamos encontrar o valor das forças que agem em cada uma das barras. Tomemos primeiramente o nó e façamos a mesma análise de forças que fizemos para encontrar as reações de apoio, dessa forma teremos
Para o nó teremos o seguinte
