Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 103
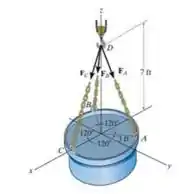
Se a resultante das três forças é , determine a intensidade da força em cada corrente.
Passo 1
Cara, para achar a intensidade da força em cada corrente a gente vai precisar achar a resultante dessas forças em função de suas intensidades , e , e igualar a resultante que o enunciado deu.
Para achar uma expressão para a força resultante, a gente vai precisar escrever nossas forças como vetores e depois somar cada componente separadamente.
E para escrever nossas forças como vetores, a gente precisa encontrar vetores unitários no sentido delas, e multiplicá-los pelo módulo da força. Basicamente usar a fórmulinha:
Como o vetor precisa ser unitário, ali a gente divide o vetor no sentido da força pelo seu módulo. Vamos fazer isso para as nossas forcinhas!
Vamos primeiro achar as coordenadas dos pontos do nosso sistema. Para
Agora para achar as outras a gente precisa usar trigonometria. e tem coordenada . Então o que a gente precisa focar é achar e . Vamos desenhar esse plano:
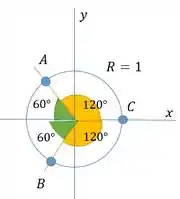
Daí a gente tira
Passo 2
Feito isso, a gente pode achar os vetores unitários nas direções das forças. Como? Para a força , que tem o sentido que sai de e vai para , a gente pode achar o vetor fazendo o ponto final menos o inicial, assim:
Aí para achar o vetor normal, a gente divide esse cara pelo módulo dele:
Fazemos o mesmo para as outras forças. sai de e vai para :
E sai de e vai para :
Passo 3
Então os vetores de força são
Passo 4
Sendo assim, nossa será dada por
Comparando o lado esquerdo com o lado direito em termos das componentes vamos ter o seguinte sistema
Resolvendo esse sistema, encontramos